Курсовая работа: Расчет выпрямительного диффузионного диода

После определения плотностей тока насыщения и генерационного тока рассчитывается повторяющийся импульсный обратный ток диода

. (1.5.14)

Площадь S, входящая в это выражение, в случае выпрямительного элемента с фаской отличается от S_АКТ для прямого направления. Обратный ток диода формируется в области объемного заряда, и в качестве S необходимо брать площадь структуры в плоскости металлургического перехода (пунктирная линия на рисунке 1.4.2), что практически совпадает с площадью большего омического контакта:

. (1.5.15)

2. РАССЧЕТНАЯ ЧАСТЬ

2.1 Расчет удельного сопротивления исходного кристалла

В качестве исходного материала выбираем кремний n-типа проводимости.

Выбор удельного сопротивления исходного кристалла производится то напряжению лавинного пробоя.

Напряжение лавинного пробоя определяется по заданному значению повторяющегося импульсного обратного напряжения U_rrm . В соответствии с формулой (1.2.1), задавшись коэффициентом запаса k = 0.80, найдем напряжение лавинного пробоя:

В .

Так как мы имеем дело с диффузионным p-n– переходом, распределение примеси в котором аппроксимируется экспонентой, то следует уточнить напряжение лавинного пробоя. Для этого сначала по формуле (1.2.9б) в первом приближении определим ширину области объемного заряда при напряжении лавинного пробоя:

мкм.

Далее, выбрав λ = 8 и сравнив l_B с 5λ, из (1.2.8б) в первом приближении определим значение концентрации легирующей примеси в исходном кристалле:

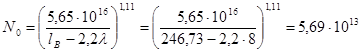см^-3 .

Имея значения параметров l_B , λ и N₀ в первом приближении, по выражению (1.2.7) можно уточнить напряжение лавинного пробоя экспоненциального p—n-перехода.

В.

Определим расхождение значения напряжения лавинного пробоя полученного по (1.2.1) с тем же полученным по (1.2.7):

Учитывая то, что расхождение меньше 3%, то расчет на этом можно закончить и установить удельное сопротивление ρ исходного кристалла. По графику зависимости удельного сопротивления от концентрации легирующей примеси [2], находим, что для N₀ = 5,69×10¹³ – ρ = 70 Ом×см.

2.2 Расчет геометрических размеров слоев выпрямительного элемента

Расчет геометрических размеров слоев диффузионного выпрямительного элемента проведем, используя приближение экспоненциального перехода.

Из рисунка 1.2.1 видно, что слоями нашей конструкции выпрямительного элемента являются p⁺ n и n⁺ слои, для расчета которых необходимо определить x_j , d_n и x_jn .

Глубину залегания p - n перехода x_j можно рассчитать используя выражение (1.3.1) откуда:

мкм, Примем x_j = 55мкм.

Тогда из (1.2.3) можно определить параметры диффузии Dt:

см^-2 .

Далее, для определения d_n найдем расширение ООЗ в n-область по (1.3.2)

мкм.

Так как l_nB много больше 150 мкм то расширение ООЗ в базу ограничим и примем: