Курсовая работа: Расчетные схемы механической части электропривода

М_с =|M_c | sign w. (1.17)

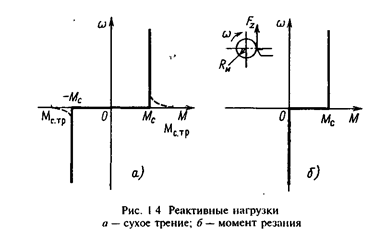
Характеристика w=f(M_с ) для нагрузки типа сухого трения показана на рис.1.4,a. В реальных механизмах эта характеристика может иметь более сложный вид из-за того, что в момент трогания силы трения могут превышать их значения при движении. Эта особенность реальных сил и моментов сухого трения отмечена на рис.1.4,a штриховыми линиями и значениями момента трогания ±М_{с тр} .

Реактивные нагрузки, возникающие при различных технологических процессах обработки, могут иметь одно направление, скачком изменяя свое значение до нуля при изменении знака скорости. Примером может служить показанная на рис.1.4,б зависимость момента резания от скорости при обработке изделия резцом, как схематически это показано на рисунке. Значение статического момента при этом пропорционально усилию резания F_Z .

M_c =F_z ·R_и

где R_и - радиус изделия.

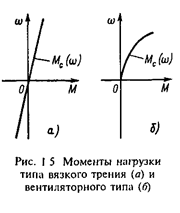
Силы и моменты вязкого трения линейно зависят от скорости:

M_с =b_вт ·w, (1.18)

где b_вт - коэффициент пропорциональности (рис.1.5,a).

Нагрузка электропривода типа вязкого трения (1.18) на практике встречается редко, чаще всего ее можно наблюдать в виде слабой линейной составляющей в нагрузке типа сухого трения. Существенное влияние на динамические процессы в механической системе оказывают силы внутреннего вязкого трения, пропорциональные скорости деформации валов, канатов, муфт и других элементов. Момент внутреннего вязкого трения можно записать в виде (см. рис 1.2,б)

M_вт =b_вт (w₁ -w₂ ) (1.19)

где w₁ и w₂ - скорости на входе и выходе деформируемого элемента; b_вт - коэффициент пропорциональности.

По характеру влияния на механические колебания в механике все силы и моменты делятся на консервативные и диссипативные.

??????????????? ?????????? ???? ? ???????, ??? ??????????? ??????? ?? ??????? ?? ?????????? ?????????? ??????? ?????????. ?????? ???????? ????, ?? ????????? ?? ????????, ? ????????? ???? ???????, ?????? ??????? ?? ?????? ????????? ???????? ?????? ????? ????. ?????????????? ?????????? ???? ? ???????, ??? ??????????? ??????? ?? ??????? ?????????? ?????????? ??????? ?????????. ?????? ?????? ???????? ???????? ????????????? ???? (???????), ??? ??? ? ???????????? ? (1.18) ??? ????????? ????? ???????? ?????????? ? ???? ???????, ? ???????????? ???????? ????????? ????????????? ????, ??? ????????????? ?????????? ??????? ?????????. ??????? ?? ???????? ????????????????? ???????? ????????, ????????? ?? ???????? ? ????? ??????? ???????:

M_с =b_мех w" (1.20)

При n=2 нагрузка называется вентиляторной (рис.1.5,б). Такой зависимостью нагрузки от скорости обладают центробежные вентиляторы. Для ряда механизмов показатель степени n>2; например такую характеристику имеют центробежные насосы, работающие на противодавление.

Существенное влияние на динамические процессы оказывают нагрузки, являющиеся периодической функцией угла поворота рабочего органа механизма. В приведенной схеме они зависят от утла поворота двигателя, например

M_c =M_max Sin w. (1.21)

Причиной возникновения таких нагрузок являются особенности технологического процесса. Их появление можно представить себе, если в механической схеме резания, приведенной на рис.1.4,б, предположить, что заготовка имеет в сечении овальную форму. Появление периодических нагрузок могут вызывать нелинейные кинематические связи типа кривошипно-шатунных, кулисных и других механизмов, у которых периодической функцией угла поворота двигателя является радиус приведения r_1j .

Во всех случаях, когда скорость двигателя при работе с такими нагрузками изменяется мало и приближенно может быть принята постоянной, для упрощения анализа периодические нагрузки рассматривают как функции времени:

где w_сp - средняя за период колебаний нагрузки скорость электропривода; k - коэффициент пропорциональности, связывающий частоту колебаний нагрузки с угловой скоростью двигателя.

Нагрузки реальных электроприводов обычно содержат в качестве составляющих рассмотренные типовые нагрузки. Так, в нагрузке электропривода реальной подъемной лебедки, кроме показанной на рис.1.3,а, активной составляющей, содержится момент потерь в двигателе и передачах, который имеет вид момента сухого трения со слабой вентиляторной составляющей, обусловленной наличием самовентиляции двигателя.

При вычислении приведенного статического момента М_с формулы (1.13) и (1.14) удобны для использования в тех случаях, когда все действующие в механизме силы и моменты определены. Обычно потери на трение в механизме неизвестны, и для их учета используется КПД механизма

h_мех =h₁ ·h₂ ·h₃ ….,

где h_1, h₂ , h₃ - КПД элементов кинематической цепи.

Если известен полезный момент нагрузки механизма M_мех , то для прямого направления энергии приведенный к валу двигателя момент статической нагрузки может быть определен из равенства

Следовательно,

где DM - момент механических потерь в двигателе; i₀ =w₁ /w_мех =i₁ i₂ i₃ …- общее передаточное число от двигателя к рабочему органу механизма. При обратном направлении потока энергии, когда нагрузка является активной, движущей и двигатель должен работать в тормозном режиме, уравнение баланса мощностей с помощью КПД передач можно записать так:

В этом случае

Момент механических потерь в двигателе невелик, составляет 1-5% номинального момента двигателя, причем большие значения его соответствуют двигателям небольшой мощности. Если значение DM определить трудно, его можно ориентировочно оценить по этим данным. Во многих практических случаях в (1.24) и (1.26) полагают DM=0, так как точность определения момента M_мех невелика, и он рассчитывается с некоторым запасом, при этом формулы приведения момента статической нагрузки к валу двигателя принимают вид:

для прямого направления передачи энергии (двигательный режим работы двигателя)