Курсовая работа: Распознавание слов естественного языка с использованием нейросетей

1.2 Модель многослойного персептрона с обучением по методу обратного распространения ошибки

Когда в сети только один слой, алгоритм ее обучения с учителем очевиден, так как правильные выходные состояния нейронов единственного слоя заведомо известны, и подстройка синаптических связей идет в направлении, минимизирующем ошибку на выходе сети. По этому принципу строится, например, алгоритм обучения однослойного персептрона. В многослойных же сетях оптимальные выходные значения нейронов всех слоев, кроме последнего, как правило, не известны, и двух или более слойный персептрон уже невозможно обучить, руководствуясь только величинами ошибок на выходах НС.

Ф. Розенблаттом использовал в своем персептроне не дифференцируемую ступенчатую функцию активации. Возможно, именно это помешало ему найти эффективный алгоритм обучения, хотя сам термин Back Propagation восходит к его попыткам обобщить свое правило обучения одного нейрона на многослойную сеть.

Разберем этот ключевой для нейрокомпьютинга метод несколько подробнее.

Алгоритм обратного распространения - это итеративный градиентный алгоритм, который используется с целью минимизации среднеквадратичного отклонения текущего выхода многослойного персептрона и желаемого выхода.

Алгоритм обратного распространения используется для обучения многослойных нейронных сетей с последовательными связями. Нейроны в таких сетях делятся на группы с общим входным сигналом - слои. На каждый нейрон первого слоя подаются все элементы внешнего входного сигнала. Все выходы нейронов m-го слоя подаются на каждый нейрон слоя m+1. Нейроны выполняют взвешенное суммирование элементов входных сигналов. К сумме элементов входных сигналов, помноженных на соответствующие синаптические веса, прибавляется смещение (порог) нейрона. Над результатом суммирования выполняется нелинейное преобразование - функция активации (передаточная функция). Значение функции активации есть выход нейрона.

На рисунке 1 показана укрупненная схема многослойной сети (многослойного персептрона). Нейроны представлены кружками, связи между нейронами - линиями со стрелками.

Рисунок 1 - Многослойный персептрон

Обозначим входы n-го слоя нейронов , весовые коэффициенты w_ij . Нейроны этого слоя вычисляют соответствующие линейные комбинации a_i :

(1)

и передают их на следующий слой, пропуская через нелинейную функцию активации:

. (2)

Нелинейная функция f называется активационной и может иметь различный вид, как показано на рисунке 2. Одной из наиболее распространенных является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид (т.е. функция S-образного вида):

(3)

При уменьшении a сигмоид становится более пологим, в пределе при a=0 вырождаясь в горизонтальную линию на уровне 0.5, при увеличении a сигмоид приближается по внешнему виду к функции единичного скачка с порогом T в точке x=0. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0,1]. Одно из ценных свойств сигмоидной функции – простое выражение для ее производной.

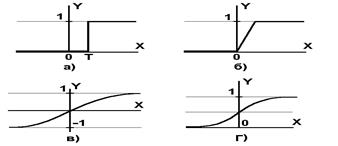
Рисунок 2 - а) функция единичного скачка; б) линейный порог (гистерезис); в) гиперболический тангенс; г) сигмоид

Следует отметить, что сигмоидная функция дифференцируема на всей оси абсцисс, что используется в некоторых алгоритмах обучения. Кроме того она обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыщение от больших сигналов, так как они соответствуют областям аргументов, где сигмоид имеет пологий наклон.

Для построения алгоритма обучения необходимо знать производную ошибки по каждому из весов сети:

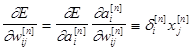. (4)

Таким образом, вклад в общую ошибку каждого веса вычисляется локально, простым умножением невязки нейрона на значение соответствующего входа. (Из-за этого, в случае, когда веса изменяют по направлению скорейшего спуска , такое правило обучения называют дельта-правилом.)

Входы каждого слоя вычисляются последовательно от первого слоя к последнему во время прямого распространения сигнала:

, (5)

а невязки каждого слоя вычисляются во время обратного распространения ошибки от последнего слоя (где они определяются по выходам сети) к первому:

. (6)

Области применения многослойных персептронов, с обучением по методу обратного распространения:

- распознавание образов;

- классификация;

- прогнозирование;