Курсовая работа: Распределение интенсивности света при дифракции на круглом отверстии

4. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Целесообразно, для круглого отверстия, использовать полярные координаты вместо прямоугольных. Пусть – полярные координаты произвольной точки отверстия:

(4.1)

(ω, ψ) – координаты точки P в дифракционной картине, относящейся к геометрическому изображению источника, т.е.

(4.2)

Из определения полярных координат следует: ω =

Запишем интеграл, описывающий дифракцию Фраунгофера (полное возмущение в точке P), в виде

(4.3)

здесь C – величина, определяющаяся через величины связанные с положениями источника и точки наблюдения, однако, на практике она удобнее выражается через другие величины.

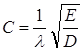(4.4)

λ – длина световой волны;

E – полная энергия, падающая на отверстие;

D – площадь отверстия ;

a – радиус отверстия;

k – волновое число .

Т.к. интенсивность выражается формулой:

(4.5)

интенсивность в центре картины (p = 0,q = 0) равна

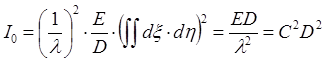(4.6)

5. РЕШЕНИЕ, АНАЛИЗ РЕЗУЛЬТАТОВ

Решение поставленной задачи произведем по методу, изложенному в [1].

Если a принять за радиус круглого отверстия, то дифракционный интеграл (4.3) примет вид

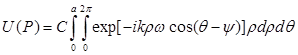(5.1)

Теперь используя интегральное представление функций Бесселя (5.2)

(5.2)

сведем уравнение (5.1) к

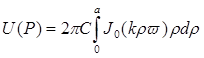(5.3)

используя рекуррентное свойство бесселевых функций (5.4)

(5.4)