Курсовая работа: Распределение интенсивности света при дифракции на круглом отверстии

(5.5)

из (5.3) и (5.5) следует, что

(5.6)

,где D = p·a2. Следовательно, интенсивность определяется выражением

(5.7)

,где I0 = C2D2 = ED/λ2 – в соответствии с (4.6)

Распределение интенсивности в окрестности геометрического изображения описывается функцией , график которой приведен в приложении 1.

Она имеет главный максимум y = 1 при x = 0 и с увеличением x осциллирует с постепенным уменьшением амплитуды подобно функции распределения интенсивности при дифракции на прямоугольном отверстии.

Интенсивность равна нулю (минимум) при значениях x, определяемых J1(x) = 0. Положения вторичных максимумов определяются значениями x, удовлетворяющими уравнению 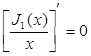, или, используя формулу (5.4) – корнями уравнения J2(x) = 0.

Минимумы и максимумы не строго эквидистантны, при увеличении x, расстояния между последовательными максимумами или минимумами приближаются к p (см. рис.2. приложения 1)

Корни уравнения J1(x) = J2(x) = 0 для нахождения минимумов и максимумов функции приведены в табл.5.1.