Курсовая работа: Разработка динамических моделей для транспортно-производственной системы

Целевая функция связывает между собой различные величины модели. Как правило, в качестве цели выбирается экономический показатель (прибыль, рентабельность, себестоимость, валовая продукция и т.д.). Поэтому целевую функцию иногда называют экономической, критериальной. Целевая функция – функция многих переменных величин и может иметь свободный член.

Критерии оптимальности – экономический показатель, выражающийся при помощи целевой функции через другие экономические показатели. Одному и тому же критерию оптимальности могут соответствовать несколько разных, но эквивалентных целевых функций. Модели с одной и той же системой ограничений могут иметь различные критерии оптимальности и различные целевые функции.

Решением экономико-математической модели, или допустимым планом называется набор значений неизвестных, который удовлетворяет ее системе ограничений. Модель имеет множество решений, или множество допустимых планов, и среди них нужно найти единственное, удовлетворяющее системе ограничений и целевой функции. Допустимый план, удовлетворяющий целевой функции, называется оптимальным. Среди допустимых планов, удовлетворяющих целевой функции, как правило, имеется единственный план, для которого целевая функция и критерий оптимальности имеют максимальное или минимальное значение. Если модель задачи имеет множество оптимальных планов, то для каждого из них значение целевой функции одинаково.

Если экономико-математическая модель задачи линейна, то оптимальный план достигается в крайней точке области изменения переменных величин системы ограничений.

Таким образом, для принятия оптимального решения любой экономической задачи необходимо построить ее экономико-математическую модель, по структуре включающую в себе систему ограничений, целевую функцию, критерий оптимальности и решение.

Для моделирования транспортно-производственных систем используется задачи линейного программирования, а именно транспортные задачи. Общая формулировка задачи имеет следующий вид: пусть осуществляется производство некоторого товара в пунктах A₁ , A₂ ,…,A_m . Объем производства товара в каждом пункте равен соответственно a₁ ,a₂ ,…,a_m . Товар необходимо доставить в магазины или потребителям, находящимся в других населенных пунктах: B₁ ,B₂ ,…,B_n . Известна потребность каждого потребителя в товаре: b₁ ,b₂ ,…,b_n . Задана также стоимость C_ij транспортировки товара из каждого пункта производства A_i каждому потребителю B_j . Требуется составить план завоза товара в магазины, обеспечивающий удовлетворение их спроса при минимальных транспортных издержках.

Методика построения экономико-математической модели состоит в том, чтобы экономическую сущность задачи представить математически, используя различные символы, переменные и постоянные величины, индексы и другие обозначения. Все условия задачи необходимо записать в виде уравнений или неравенств. Поэтому, в первую очередь необходимо определить систему переменных величин, которые могут для конкретной задачи обозначить искомый объем производства продукции на предприятии, количество перевозимого груза поставщиками конкретным потребителям [4].

2.2 Формальная постановка и математическая запись.

Оптимизационная задача – это экономико-математическая задача, которая состоит в нахождении оптимального (максимального или минимального) значения целевой функции, причем значения переменных должны принадлежать некоторой области допустимых значений.

Выше описаны условия задачи, которая может быть сведена к решению так называемой однопродуктовой многоэтапной транспортно-производственной модели. Рассматривается один продукт, который от пункта производства до конечного потребителя проходит несколько стадий транспортировки и переработки. Путем несложных преобразований, такую модель можно свести к классической транспортной задаче, методы решения которой описан ниже.

Формальная постановка и математическая запись задачи.

Дано:

A_i – множество наименований поставщиков;

B_j – множество наименований потребителей;

a_i - объем произведенной продукции в i -ом пункте(I  N);

b_j - платежеспособный спрос на продукцию в j-ом пункте (j  M);

C_ij - затраты на транспортировку единицы продукции от i-го поставщика j-му потребителю.

Требуется найти такие объемы транспортировки продукции от каждого поставщика к каждому потребителю ( x_{i , j} > 0, для i = N и j = M) ), при которых достигается минимум транспортных затрат (что при фиксированных ценах реализации продукции равносильно максимизации прибыли), то есть:

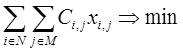(1.1)

При этом должны соблюдаться условия:

- продукции должно быть вывезено не более произведенного количества:

, (1.2)

- платежеспособный спрос должен покрываться:

, (1.3)

Рассмотрим один из методов решения транспортной задачи – метод потенциалов, основанный на идее последовательного улучшения допустимого решения. В методе потенциалов, как и во многих других методах оптимизации, используется следующий прием: строится система оценок (цен-измерителей), позволяющая определить, является ли построенный план оптимальным (другими словами, построить признак оптимальности). Применительно к транспортной задаче признак оптимальности формулируется следующим образом: допустимый план перевозок тогда и только тогда является оптимальным, когда каждому пункту производства и потребления можно поставить в соответствие оценки (потенциалы), удовлетворяющие двум условиям:

Во-первых, разность оценок пунктов потребления ( v_j ) и производства ( u_i ), между которым запланированы перевозки, равна затратам на транспортировку единицы продукта ( C_{i , j} ) между этими пунктами, т.е.

v_j – u_i = c_{i , j} . для x_{i , j} > 0

Во-вторых, аналогичные разности для всех остальных направлений (не вошедших в план) не превосходят затрат на транспортировку.

v_j – u_i < C_{i , j} . для x_{i , j} = 0