Курсовая работа: Разработка факультатива "Оптимальный портфель ценных бумаг"

Пусть в группе В играли пять команд по круговой системе. Результаты игры отображены в таблице.

Где 2- победа,1- ничья,0- поражение.

Эту таблицу также можно назвать матрицей.

Опр. Таблицу вида

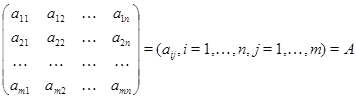
будем называть матрицей размерности .

Для краткости будем обозначать матрицы большими латинскими буквами.

Вектор является частным случаем матрицы при m=1.

1.3.3 Умножение матриц. Свойства

Как сложить две матрицы?

Опр. Суммой матриц и размерности называется матрица размерности .

Пример.

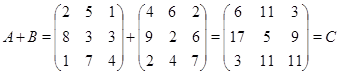
Как суммировать матрицы вы уже знаете. Теперь придумайте как умножить матрицу на число.

Опр. Произведением матрицы размерности и числа называется матрица размерности .

Пример.

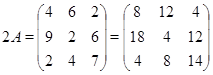
Кроме введенных операций нам понадобится умножение матриц.

Опр. Произведением матриц и называется матрица , где

Необходимо показать и озвучить практический способ умножения матриц: строка умножается на столбец. Берем первую строку матрицы А, ставим ее вертикально напротив первого столбца матрицы В, умножаем элементы этой строки и столбца, которые стоят напротив др.др., складываем произведения. Это первый элемент матрицы С. Теперь таким же образом умножаем эту строку на второй столбец - получаем второй элемент первой строки матрицы С. И т.д. Получим первую строку новой матрицы. Для того, чтобы получить вторую строку, проделываем тоже самое со второй строкой матрицы А.

Пример.

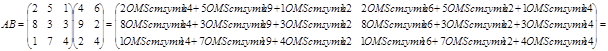
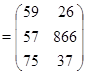
Задача 1. Выполнить умножение.