Курсовая работа: Разработка имитационной модели транспортной сети
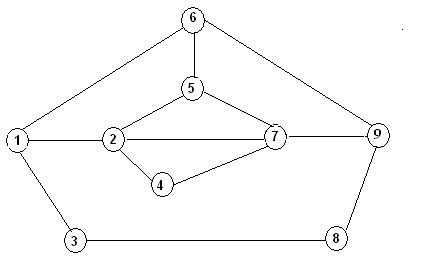
Рисунок 2.1.1 - Граф железнодорожной сети
Узлы - это города, через которые проходит сеть дорог. Дуги - это участки пути, соединяющие соответствующие города. Каждая дуга имеет свою пропускную способность. В сети кроме транзитных потоков существуют внутренние транспортные потоки, которые значительно снижают пропускную способность участка сети дорог. В каждом узле происходят процессы формирования и расформирования составов.
Пусть имеется один узел отправления и один узел назначения. Требуется определить с учётом структуры сети и имеющихся параметров максимальный поток в сети с минимальными затратами всех ресурсов. Таким образом, ставится задача определения с помощью имитационной модели максимального потока между начальным и конечным узлом графа, поиск узких мест в сети, устранение которых позволит достичь оптимальной организации потоков в железнодорожной сети.
Эта задача решается следующим образом. Для получения усредненных характеристик максимального потока и его “выгоды" необходимо провести N прогонов.
На первой итерации применения процедуры Монте-Карло вероятностная задача поиска максимального потока в сети превращается в классическую. При этом определяются компоненты матрицы пропускных способностей путём вычисления cijl =cij -vijl , где vijl определяется по функции распределения Hij (v) путём нахождения единичного жребия третьего типа.
При учёте влияния внутренних потоков на пропускные ситуации в сети возможны следующие ситуации:
внутренних потоков нет на участке дороги;
внутренние потоки влияют на пропускную способность участка таким образом, что она уменьшается, но остаётся больше либо равна значению потока на этом участке, т.е. ![]() , где
, где ![]() - пропускная способность сети изменённая с учётом внутренних потоков (при этом алгоритм Форда-Фалкерсона работает и находится максимальный поток и его распределение по ветвям сети);
- пропускная способность сети изменённая с учётом внутренних потоков (при этом алгоритм Форда-Фалкерсона работает и находится максимальный поток и его распределение по ветвям сети);
внутренние потоки влияют на пропускную способность участка таким образом, что она уменьшается и становится меньше значения потока на этом участке, т.е. ![]() , где
, где ![]() - пропускная способность сети изменённая с учётом внутренних потоков (в этих условиях алгоритм Форда Фалкерсона не работает и данная ситуация говорит о возникновении “пробки" в сети на этом участке).
- пропускная способность сети изменённая с учётом внутренних потоков (в этих условиях алгоритм Форда Фалкерсона не работает и данная ситуация говорит о возникновении “пробки" в сети на этом участке).
Для каждого i-го узла сети с учётом заданных функций распределения времён формирования-расформирования вычисляется среднее время нахождения в i-ом узле транспортной единицы. В качестве начального потока выбираются значения матрицы ![]() .
.
На k-ой итерации (k - номер итерации в алгоритме Форда-Фалкерсона) с помощью алгоритма Форда-Фалкерсона, используя изменённую матрицу пропускных способностей определяется само распределение потока по сети и его значение потока. По формулам (1.2), (1.3), и (1.4) с учётом распределения потоков, определяется обобщённый показатель “выгоды" этого потока. Значения потока, матрица значений распределения потока по ветвям и показатель “выгоды" запоминаются в базе данных модели (БДМ). Модифицируется номер итерации процедуры Монте-Карло (l=l+1) и все расчёты повторяются сначала.
По завершении N итераций этих расчётов в БДМ модели сформированы следующие выборки: выборка матриц распределения потока по ветвям сети, то есть для каждого элемента матрицы распределений потока имеется своя выборка; выборка значений максимального потока; выборка интегральных показателей “выгоды" потока.
По этим выборкам объема N формируются средние значения, а именно:
![]() ;
; ![]() ;
; ![]()
Все эти значения должны быть вычислены и представлены пользователю по завершении работы программы.
Для поиска узких мест в Gh с начальным пунктом Z и конечным пунктом Y проведём покомпонентное вычитание из этой матрицы соответствующих значений матрицы пропускных способностей Сh::
![]()
В тех местах, где элементы этой матрицы будет иметь отрицательное значение, находятся “узкие места" в Gh . На величину этой разности пропускные способности сij должны быть увеличены для того, чтобы граф Gh обеспечивал максимальный поток транзитных маршрутов в направлении из точки Z в точку Y.
Таким образом, по завершении работы программы, также должны быть получены следующие значения: матрица, характеризующая узкие места в сети, и рекомендуемая матрица пропускной способности для данной сети дорог.
Алгоритм работы модели основан на сочетании процедуры Монте-Карло и теоремы Форда-Фалкерсона и применением единичного жребия третьего типа.
2.2 Алгоритм работы модели железнодорожной сети
Алгоритм работы модели железнодорожной сети представлен на рисунке 2.2 Для работы программного обеспечения необходимо задать следующие входные значения:
![]() - матрица пропускной способности сети;
- матрица пропускной способности сети;
![]() - матрица расстояния между узлами;
- матрица расстояния между узлами;
![]() - матрица стоимости единицы пути;
- матрица стоимости единицы пути;
![]() - функция распределения времени на формирование и расформирование составов;
- функция распределения времени на формирование и расформирование составов;
![]() - вектор времени на формирование и расформирование составов;
- вектор времени на формирование и расформирование составов;
![]() - количество прогонов программы.
- количество прогонов программы.