Курсовая работа: Разработка имитационной модели
Названные выше этапы имитационного исследования редко выполняются в строго заданной последовательности, начиная с определения проблемы и кончая документированием. В ходе имитационною исследования могут быть сбои в прогонах модели, ошибочные допущения, от которых в дальнейшем приходится отказываться, пере формулировки целей исследования, повторные оценки и перестройки модели. Такой итеративный процесс позволяет разработать имитационную модель, которая дает верную оценку альтернатив и облегчает процесс принятия решения.
4. Разработка модели
В данной курсовой работе применяются следующие распределения: равномерное, нормальное, логнормальное, пуассоновское распределение. Время ответа на запрос точки магазином имеет логнормальное распределение. Спрос на товары в точке за день имеет пуассоновское распределение. Время ответа на запрос магазина фабрикой распределено нормально, а для нахождения одного нормального числа нужно найти 12 равномерно распределенных чисел.
4.1 Логико-математическое описание моделируемой системы
Нормальное распределение
Функция плотности вероятности нормального закона имеет вид:
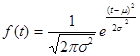
- параметры нормального закона, (
- среднее значение, 
- дисперсия нормального распределения).
Генератор нормально распределенной случайной величины X можно получить по формулам:
где Tj (j=1,…,12) – значения независимых случайных величин, равномерно распределенных на интервале (0,1).
Равномерное распределение
Функция плотности вероятности равномерного распределения задает одинаковую вероятность для всех значений, лежащих между минимальным и максимальным значениями переменной. Другими словами, вероятность того, что значение попадает в указанный интервал, пропорциональна длине этого интервала. Применение равномерного распределения часто вызвано полным отсутствием информации о случайной величине, кроме ее предельных значений. Равномерное распределение называют также прямоугольным.
при 
.
Среднее значение распределения равно
,
дисперсия равна
.
Равномерно распределенная случайная величина X на отрезке [a,b] выражается через равномерно распределенную на отрезке [0,1] случайную величину R формулой
.
Логнормальное распределение
Метод получения случайного выборочного значения Y=eX , где X – нормальное распределение случайной величины с дисперсией 
и средним значением 
Распределение Пуассона
Для получения пуассоновски распределенной случайной величины Y можно воспользоваться следующим методом:
,
где Rn – n-е псевдослучайное число.
4.2 Формализованная схема объекта моделирования
обслуженный запрос выполненный заказ
запрос заказ