Курсовая работа: Разработка программного обеспечения для решения уравнений с одной переменной методом Ньютона (касательных)

если (a*ln(b*n) *(-a/sqr(n))) > 0 то

mass [i]: =n;

code_of: =1;

иначе

вывод

number: =0; code_of: =0;

если (code_of = 1) то

выполнять

x1: =mass [i] -a*ln(b*mass [i]) /

(a/mass [i]);

root: =Abs (x1-mass [i]);

i: =i+1;

mass [i]: =x1;

пока (root < E);

если (x1 < m) или (x1 > n) то

вывод

number: =0; code_of: =0;

вывод

Рисунок 5.4 – Алгоритм решения уравнения вида y(x) =a×ln(b×x) (продолжение)

5.7.2. Алгоритм нахождения корня уравнения y(x) =a×x2+b×x+c

Алгоритм решения уравнения вида y(x) =a×x2+b×x+c приводится на рисунке 5.5.

выполнять

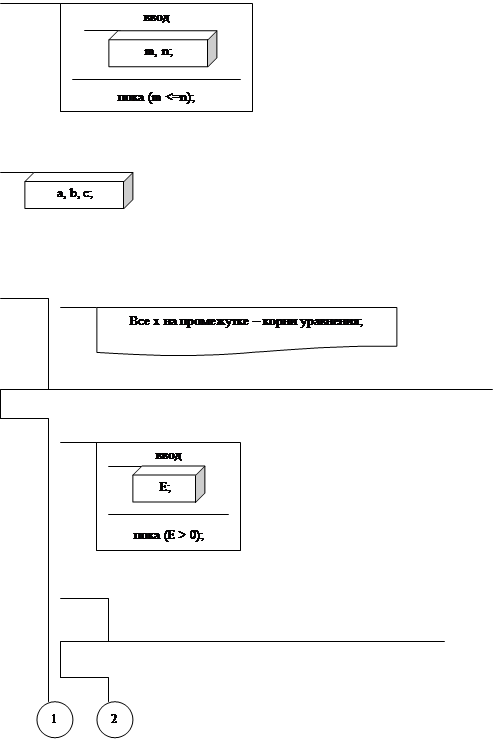
ввод

если (a = 0) и (b = 0) и (c = 0) то

вывод

number: =0;

иначе

выполнять