Курсовая работа: Разработка сменного модуля для изучения резистивного соединения типа Треугольник
Четырехполюсники делятся на симметричные и несимметричные . В симметричном четырехполюснике перемена местами входных зажимов не изменяет напряжений и токов в цепи, с которой он соединен. Четырехполюсники, кроме электрической симметрии, могут иметь структурную симметрию, определяемую относительно вертикальной оси симметрии. Так, Т – образный, П – образный и Т – перекрытый четырехполюсники имеют вертикальную ось симметрии при Z1 =Z3 . Мостовая схема структурно симметрична. Очевидно, четырехполюсники, симметричные в структурном отношении, обладают электрической симметрией.
Четырехполюсники могут быть уравновешенными и неуравновешенными . Уравновешенные четырехполюсники имеют горизонтальную ось симметрии (например, мостовая схема на рис. 2) и используется, когда необходимо сделать зажимы симметричными относительно какой-либо точки (например – земли). Можно сделать уравновешенной любую из лестничных схем четырехполюсников.
Четырехполюсники также делятся на обратимые и необратимые . Обратимые четырехполюсники позволяют передавать энергию в обоих направлениях; для них справедлива теорема обратимости или взаимности, в соответствии с которой отношение напряжения на входе к току не меняется при перемене местами зажимов.
1.2 Уравнения передачи четырехполюсников
Основной задачей теории четырехполюсников является установление соотношений между четырьмя величинами: напряжениями на входе и выходе, а также токами, протекающими через входные и выходные зажимы. Уравнения, дающие зависимость между U1 , U2 , I1 , и I2 , называются уравнениями передачи четырехполюсника . Для линейных четырехполюсников эти уравнения будут линейными. Величины, связывающие в уравнениях передачи напряжения и токи, называются параметрами четырехполюсника .
Сложная электрическая цепь, имеющая входные и выходные зажимы, может рассматриваться как совокупность четырехполюсников, соединенных по определенной схеме. Зная параметры этих четырехполюсников, можно вычислить параметры сложного четырехполюсника и получить тем самым зависимость между напряжениями и токами на зажимах результирующего сложного четырехполюсника, не производя расчетов всех напряжений и токов внутри заданной схемы.
Кроме того, теория четырехполюсников позволяет решить обратную задачу: по заданным напряжениям и токам найти параметры четырехполюсника и затем построить его схему и рассчитать элементы, т.е. решить задачу синтеза.
Например, если к вторичным выводам четырехполюсника подключен приемник с сопротивлением нагрузки Zн , а к первичным – источник ЭДС Е1 (рис. 1), то при заданном напряжении на выводах приемника U2 и токе I2 =U2 /Z2 можно определить необходимое напряжение источника питания на первичных выводах U1 =E1 и ток источника I1 по уравнению:
![]() U1 =A11 U2 +A12 I2
U1 =A11 U2 +A12 I2
I1 =A21 U2 +A22 I2 (1)
Коэффициенты, входящие в систему уравнений, связывающую входные U1 и I1 и выходные U2 и I2 напряжения и токи называются А-параметрами , или обобщенными параметрами . Уравнения называются уравнениями передачи в А-параметрах . Параметры А11 и А22 являются безразмерными, параметр А12 имеет размерность сопротивления; параметр А21 – размерность проводимости.
Свойства параметров-коэффициентов
Параметры, образованные из коэффициентов уравнений передачи, объединяют одним названием параметры-коэффициенты .
Свойства:
1. Параметры-коэффициенты определяются только схемой четырехполюсника и ее элементами и не зависят от внешних цепей, между которыми может быть включен четырехполюсник, т.е. они характеризуют собственно четырехполюсник.
2. Все системы параметров-коэффициентов описывают один и тот же четырехполюсник, поэтому между различными системами параметров-коэффициентов существует однозначная взаимосвязь.
3. Пассивный четырехполюсник полностью характеризуется не более чем тремя независимыми параметрами.
4. При изменении направления передачи энергии через четырехполюсник во всех выражениях, включающих А – параметры, коэффициенты А11 и А22 меняются местами.
5. Симметричные пассивные четырехполюсники имеют только два независимых параметра. В самом деле, в случае симметричного пассивного четырехполюсника не имеет значения направление передачи энергии: напряжения и токи на входе и выходе не изменяются при замене местами зажимов.
6. Параметры-коэффициенты имеют определенный физический смысл. Для выявления этого физического смысла следует четырехполюсник поставить в такой режим работы, при котором уравнения передачи содержат лишь один интересующий нас параметр. Подобное произойдет, если использовать режимы холостого хода и короткого замыкания.
7. Из предыдущего свойства следует, что параметры-коэффициенты являются комплексными величинами, так как они определяются отношением комплексных амплитуд (действующих значений) напряжений и токов. В случае анализа четырехполюсника в режиме негармонических колебаний используют спектральные представления электрических величин. Можно показать, что параметры-коэффициенты, рассматриваемые относительно не отдельной частоты, а определенного спектра частот, являются рациональными функциями оператора jω. При переходе от оператора jω к оператору p параметры-коэффициенты представляют собой рациональные функции оператора p .
1.3 Применение матриц к расчету четырехполюсников
Любую из систем уравнений передачи четырехполюсника можно записать в матричной форме. В частности для системы уравнений в А – параметрах.
![]() U1 =A11 U2 +A12 I2
U1 =A11 U2 +A12 I2
I1 =A21 U2 +A22 I2
получим:
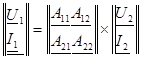 (2)
(2)
где ![]()
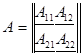 – квадратная матрица коэффициентов;
– квадратная матрица коэффициентов;
![]() и
и ![]() – матрицы-столбцы напряжения и тока соответственно на первичных и вторичных выводах.
– матрицы-столбцы напряжения и тока соответственно на первичных и вторичных выводах.