Курсовая работа: Реализация и анализ ЦФ с КИХ

Разработать цифровой согласованный фильтр (СФ) с конечной импульсной характеристикой и получить следующие его характеристики:

- спектр входного сигнала;

- спектральную (амплитудно-частотную) характеристику окна;

- АЧХ и ИХ фильтра;

- отклик фильтра на заданный сигнал;

- спектр выходного сигнала.

Проанализировать полученные результаты.

Параметры фильтра (Вариант №16):

Тип фильтра: согласованный с заданным сигналом фильтр;

Тип окна: Ханна;

Тип сигнала: прямоугольный радиоимпульс с несущей частотой, равной f_д /4, и внутриимпульсной ЛЧМ (девиация частоты равна f_д /4, база сигнала равна 30, скважность – 15).

2. Расчет фильтра

ПРИМЕЧАНИЕ: Все машинные расчеты в данном задании будут проводиться в среде MatLabv 6.5.

Так как в данном задании используется сигнал с B=20, воспользуемся формулами для ЛЧМ-сигналов с большой базой:

, где =dw – частота девиации, а = dw/ti– скорость нарастания частоты импульса.

Аналоговый сигнал имеет вид: при и 0 при .

Импульсная характеристика согласованного фильтра описывается выражением , где k – коэффициент, зависящий от физической реализации устройства (алгоритма), реализующего СФ. Для простоты анализа в дальнейшем амплитуду сигнала включим в k, и приравняем его к 1.

Далее нужно рассчитать, сколько точек необходимо для реализации согласованного фильтра. Сначала сосчитаем, сколько точек нужно для реализации радиоимпульса длиной t_и .: . Для заданного сигнала

Тогда fд выберем равной 120 Гц, а f0, равную fd/4 – соответственно 30 Гц. В этом случае максимальная частота импульса составит f0+df = 0.25Fd+0.25fd, т.е, ровно половину от частоты дискретизации: 60 Гц, следовательно теорема Котельникова будет выполнена и наложения спектров не наступит. Длительность аналогового импульса равна 1с, дискретного – 120 отсчетов (точек).

Дискретизированный сигнал имеет вид:

U_дискр (n) = U_аналог (n*T_д ):

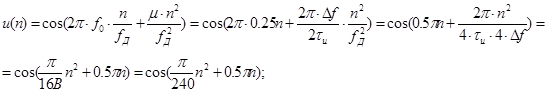
n = 0..N_и -1 = 0..119;

Далее построим выражение для импульсной характеристики фильтра:

Особенностью согласованного фильтра является то, что его импульсная характеристика h(t) является зеркальным отображением сигнала S(t) относительно прямой t=t₀ /2 (рис.1).

Рисунок 1

Это справедливо и для цифрового согласованного фильтра, поэтому:

Дискретная ИХ СФ:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--