Курсовая работа: Реализация и анализ ЦФ с КИХ
n=0..Nи -1=0..119;
так как функция cos(t) - 2p-периодическая. В MatLabже зеркальное отражение можно осуществить, если инвертировать массив отсчетов дискретизированного импульса, причем n нужно брать не от 0 до Nи -1, а от 1 до Nи , что обусловлено тем, что нумерация элементов в массивах в MatLаb ведется, начиная с единицы.
Полученная импульсная характеристика затем взвешивается окном Ханна:
w(n) = 0.5(1-cos(2π*(n-1)/(Nи -1))) на интервале ![]() причем данное окно необходимо сдвинуть вправо на
причем данное окно необходимо сдвинуть вправо на ![]() , чтобы перекрывать весь сигнал. В MatLab это окно (уже со сдвигом) строится функцией hann(Nи ).
, чтобы перекрывать весь сигнал. В MatLab это окно (уже со сдвигом) строится функцией hann(Nи ).
На выходе согласованного фильтра после появления на входе сигнала, с которым он согласован, в момент окончания сигнала tи должна появиться автокорреляционная функция(АКФ) этого сигнала. Аппроксимирующее выражение для нормированной АКФ ЛЧМ сигнала имеет вид:

В дальнейшем для определенности, амплитуду и дискретного и наналогового сигнала я беру равной 1.
Теперь приведу необходимые графики(для расчетов использована программа MatLAB):
1) Входной аналоговый и дискретизированный ЛЧМ сигналы S(t) и S(n):


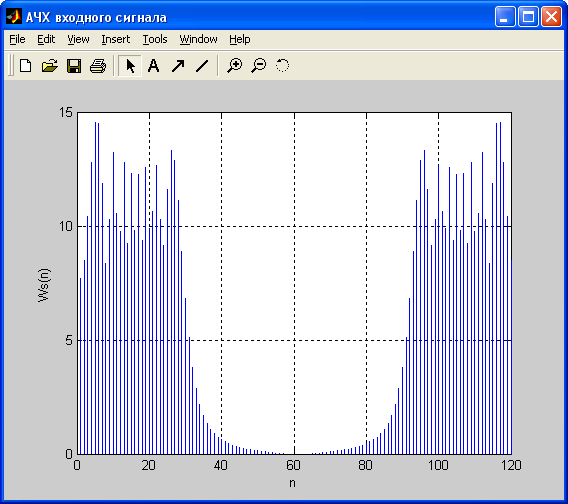
2) Амплитудный спектр (АЧХ) входного сигнала Ws(n):
3) Вид и АЧХокна:


4) ИХ взвешенного фильтра:

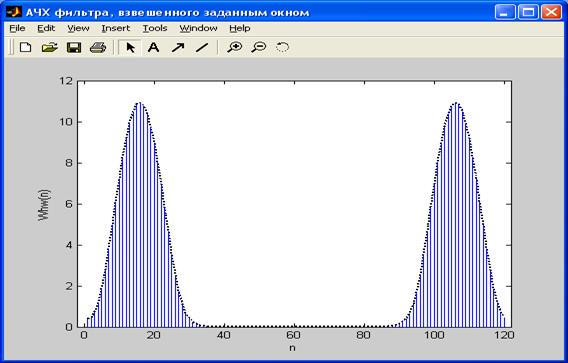
5) АЧХ взвешенного фильтра:
6) Спектр выходного сигнала (подвергшегося согласованной фильтрации). Получается перемножением спектров входного сигнала и спектра взвешенного фильтра:

7) Нормированный отклик фильтра на заданный сигнал – Kssf(tau) /tau – величина сдвига/. Отклик получен сверткой входного сигнала и ИХ взвешенного окном фильтра:
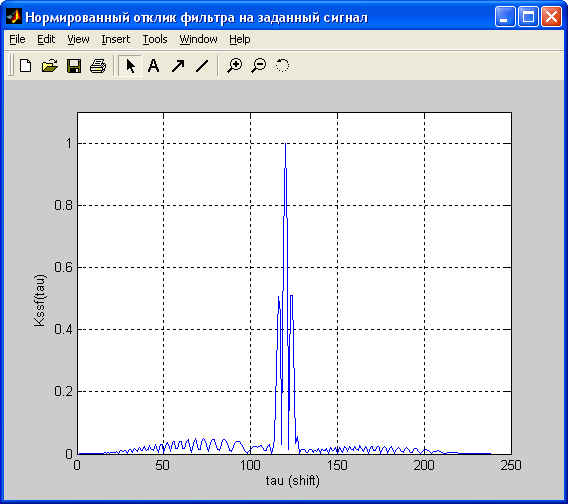
Теперь сравним полученный отклик с аппроксимацией АКФ входгого сигнала (см. следующую страницу):
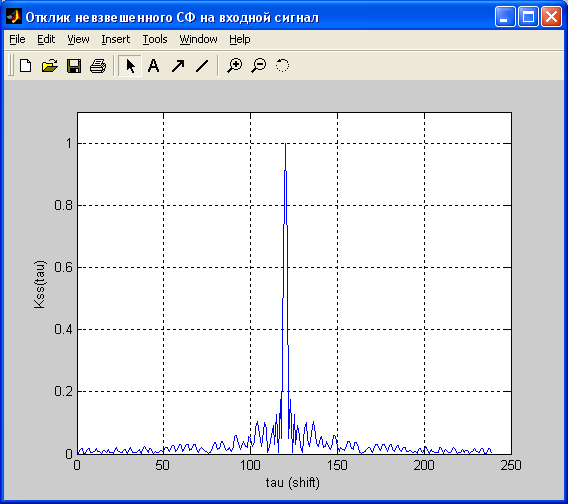
8) Смещенная на Nи АКФ входного сигнала (отклик СФ без окна на входной сигнал) Kss(tau) /tau – величина сдвига/. Отклик получен сверткой входного сигнала и ИХ ещё не взвешенного окном СФ:
ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ
В ходе выполнения настоящего домашнего задания был реализован согласованный фильтр с конечной импульсной характеристикой (КИХ – фильтр).
Коэффициенты этого КИХ-фильтра – это отсчеты его импульсной характеристики, полученной в ходе вычислений. Кроме теоретического алгоритма, приведенного мной в начале задания, разработан непосредственно машинный алгоритм реализации заданного фильтра для выполнения в среде MatLab 6.5.