Курсовая работа: Ремонт автомобиля: восстановление, массовое обслуживание, технологический процесс

Из рисунка 4 видно, что при среднем числе требований на ремонт = 3, вероятность того, что в некоторые смены число требований меньше среднего, т.е. < 3, будет 42%, равно среднему – 22%, больше среднего – 36%. Следовательно расчёт площадей производственных помещений, оборудования, рабочей силы исходя из средней потребности может вызвать или неполную загрузку оборудования или необходимость ожидания автомобилей в очереди.

В зависимости от стоимости простоя автомобиля в ожидании ремонта, а рабочей силы и оборудования в ожидании автомобилей, требующих ремонта, определяют оптимальную пропускную способность постов, участков, цехов ТО и Р. Эта задача решается с использованием теории массового обслуживания.

Характерным признаком закона Пуассона является равенство среднего и дисперсии:

. (34)

Коэффициент вариации:

. (35)

С увеличением среднего числа отказов, поступающих на посты, коэффициент вариации сокращается, и закон распределения становиться более симметричным, что благоприятно сказывается на организации ТО и Р автомобилей:

среднее число отказов 1 2 3 4 5 9 25

коэффициент вариации 1 0,71 0,58 0,50 0,45 0,30 0,22

Следовательно, централизация ТО и Р, которая приводит к увеличению программы работ, является одним из направлений совершенствования технической эксплуатации автомобилей.

2.3 Циклические процессы

Если в Марковском процессе с непрерывным временем дискретные состояния связаны между собой в одно кольцо и имеют односторонние переходы, то такой процесс называется циклическим.

S4

S3

S1

S2

Рисунок 5. Циклический процесс: S1 – автомобиль исправен и работает; S2 – автомобиль ожидает ремонта; S3 – автомобиль находится в ремонте; S4 – автомобиль исправен и ожидает работы после ремонта.

Плотности вероятностей перехода из одного состояния в другое односторонние.

Для предельных вероятностей:

. (36)

При переходе из 1-го состояния во 2-е:

; (37)

при переходе из 2-го в 3-е:

; (38)

при переходе из 3-го в 4-е:

; (39)

при переходе из 4-го в 1-е:

. (40)

Решая эту систему получим:

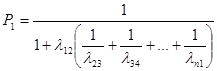; (41)

; (42)

; (43)