Курсовая работа: Решение дифференциальных уравнений по методу Эйлера
![]()
![]() хк хк1/2 xk+h =xk1 X
хк хк1/2 xk+h =xk1 X
Рисунок 3.
Через Мк проводим касательную: y=yк =f(xk ,yk )(x-xk ). Делим отрезок (xк ,xк1 ) пополам:
xh+k / =xk +h/2=xk+1/2 (9)
yh+k / =yk +f(xk ,yk )h/2=yk +yk+1/2 (10)
Получаем точку Nk / . В этой точке строим следующую касательную:
y(xk+1/2 )=f(xk+1/2 , yk+1/2 )=αk (11)
Из точки Мк проводим прямую с угловым коэффициентом αк и определяем точку пересечения этой прямой с прямой xк1 . Получаем точку Мк / . В качестве ук+1 принимаем ординату точки Мк / . Тогда:
yк+1 =yк +αк h
xk+1 =xk +h
αk =f(xk+h/2 , xk +f(xk ,yk )h/2) (12)
yk =yk-1 +f(xk-1 ,yk-1 )h
Эти формулы называются рекуррентными формулами метода Эйлера.
Сначала вычисляют вспомогательные значения искомой функции yк+1/2 в точках xк+1/2 , затем находят значение правой части уравнения (1) в средней точке
y/ k+1/2 =f(xk+1/2 , yk+1/2 ) и определяют yк+1 .
3. Блок-схема алгоритма
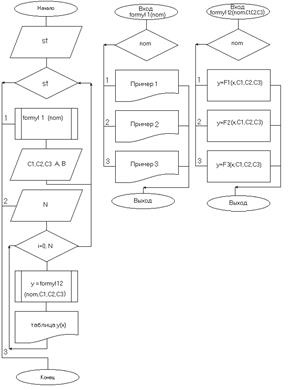
где A — начальное значение x, B — конечное значение x, F(x) — значение функции в точке xn , N — количество промежутков, st – выбор операции, C1,C2,C3 – константы для формул, nom - сохраняет номер используемой функции.
На рисунке представлена блок-схема процесса решения дифференциального уравнения методом Эйлера
Подсчитывая каждый раз новое значение уравнения F(x), получаем последовательность значений xn yn , n=1,2,…
По этим значениям строим график.
4. Описание программы
Программа весьма проста. В ней много предусмотрено моментов неправильного ввода данных, о которых программа предупреждает пользователя и сразу же просит повторно ввести данные.
С самого начала программа предоставляет пользователю меню выполняемых функций, которые выделяются при помощи стрелок ↑ и ↓ выбор клавишей Enter:
Formyla -> Enter
-> Open in fails
Reshenie
Graphic
Exit