Курсовая работа: Решение математических задач с помощью алгоритмического языка Turbo Pascal, Microsoft Excel, пакета MathCAD и разработка программ в среде Delphi

for i: =1 to n Do

begin

z: =exp ( (-x*sin (x)) *ln (x)) - ln (2*x+5);

d: =sqrt (2+sin (2*x)) +sqr (x);

F: =z/d;

S: =S+F*a [i] ;

x: =x+h;

end;

WriteLN ('S=',S: 10: 3);

readkey

END.

Результаты вычислений:

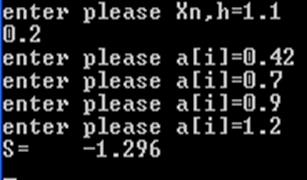
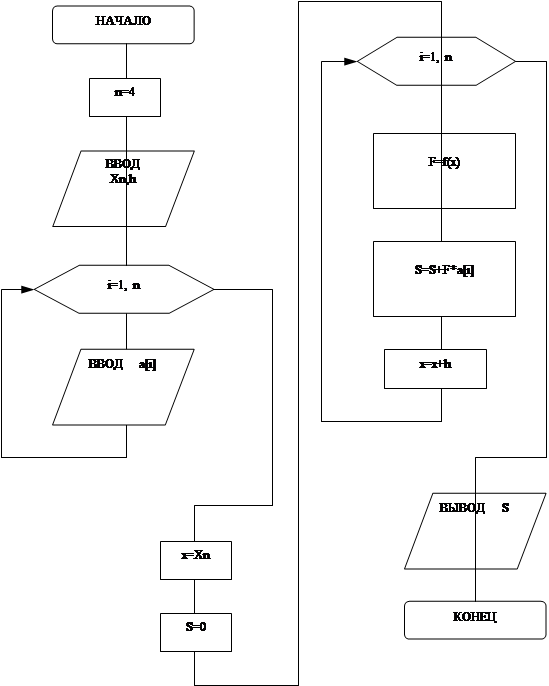
Блок-схема алгоритма решения задания №1.4

Нахождение функции, если дан x, h, n, задан массив :

Задание 2. Интегрирование функции

Вычислить определённый интеграл

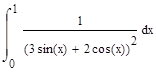
Так как определённый интеграл является площадью фигуры, ограниченной некоторой функцией y=f (x), то целью задачи является нахождение площади этой фигуры. Для этого необходимо данную фигуру разбить на более простые, площадь которых находится по простым формулам, а затем сложить полученные площади в одну для нахождения необходимой, т.е. для вычисления данного определённого интеграла.

Существуют различные методы нахождения определённого интеграла.

Рассмотрим некоторые из них:

метод средних прямоугольников;

метод трапеций;

метод Симпсона (парабол);

с автоматическим выбором шага;

1. Метод прямоугольников

Для вычисления приближённого значения определённого интеграла отрезок [a, b] делят на n равных частей точками

a=x₀ <x₁ <x₂ <…<x_n =b

так, что x_i+1 -x_i = (b-a) /n (I=0,1,2,…,n-1). Тогда длина каждого частичного отрезка определяется как h= (b-a) /n, а точки разбиения x₀ =a, x₁ =x₀ +h, x₂ =x₁ +h,…, x_n =x_{n -1} +h. Эти точки называются узлами, а h-шагом интегрирования. В узлах вычисляются ординаты y₀ , y₁ ,…, y_n , т.е. y_i =f (x_i ). На частичных отрезках [x_{i ;} x_{i +1} ] строятся прямоугольники, высота которых равна значению f (x) в какой-либо точке каждого частичного отрезка. Произведение f (x_i ) *h определяет площадь частичного прямоугольника, а сумма таких произведений - площадь ступенчатой фигуры, представляющей собой приближённое значение интеграла.

Если f (x_i ) вычисляется в левых концах отрезков [x_i ; x_{i +1} ], то получается формула левых прямоугольников:

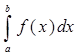»I_л = (y₀ +y_1+…+ y_{n -1} ) = .
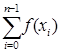