Курсовая работа: Решение математических задач с помощью алгоритмического языка Turbo Pascal, Microsoft Excel, пакета MathCAD и разработка программ в среде Delphi

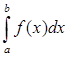»I_п = (y₁ +y_2+…+ y_n ) = .

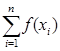Если функция f вычисляется в точках x_i +h/2Î [x_{i ;;} x_{i +1} ], то получается формула средних прямоугольников:

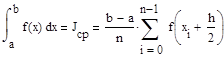
2. Метод трапеции

Метод трапеций аналогичен методу прямоугольников, с той лишь разницей, что на каждом частичном отрезке строится трапеция.

Приближенное значение интеграла равно сумме всех площадей частичных трапеций:

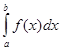»I=

3. Метод симпсона

Если на частичном отрезке длиной 2h функции заменяется дугой параболы, то можно получить формулу парабол или обобщенную формулу Симпсона:

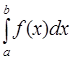= (h/3) * (y₀ +y_{2 n} +,

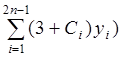где

1 при i - нечетном;

C_i =

1 при i - чётном ;

4. С автоматическим выбором шага

Точность вычисления определенного интеграла зависит от величины шага интегрирования. Ошибка в выборе величины шага интегрирования либо не обеспечит нужной точности, либо приведет к необоснованным затратам машинного времени.

Заданную точность при рациональных затратах времени на вычисления обеспечивают алгоритмы интегрирования с автоматическим выбором шага. Идея метода автоматического выбора шага интегрирования для достижения заданной точности заключается в следующем:

а) выбирается начальное n и вычисляется шаг h= ( b- a) / n ;

б) рассчитывается значение интеграла I₁ для этого шага h ;

в) шаг h уменьшается в два раза, т.е. h= h/2 и вычисляется значение интеграла I₂ ;

г) оценивается погрешность между двумя значениями r= ½ I₁ - I₂ ½ ; если погрешность r меньше или равна заданной точности, т.е. r<= e , то точность достигнута и значение интеграла I= I₂ ; если r> e , то точность не достигнута и величине I₁ присваивается более точное значение I₂ ;

д) теперь повторяются этапы в) и г) до выполнения условия r<= e .

Вычисление определенного интеграла с помощью пакета MathCAD в нормальном и символьном виде.

Для решения интеграла численно и в символьном виде необходимо задать функцию f (x) и найти от неё интеграл 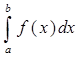на промежутке [a, b].

Для вычисления численного значения заданного интеграла:

С помощью встроенных функций задаём определённый интеграл;

После нажатия клавиши "=", MathCAD выдаёт значение интеграла на заданном промежутке.

В Mathcad: