Курсовая работа: Решение военно-логистических задач по выбору оптимального маршрута для военно-транспортных средств

Но t₁ = = 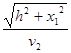, а t₂ = =

И поэтому Т== +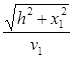

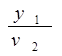
Целевая функция является нелинейной функцией двух переменных, связанных между собой соотношением вида L1=x1+y1, выступающим в качестве линейного ограничения на переменные х1 и у1. В соответствии с содержанием методом условного экстремума запишем функцию Лагранжа.

Т^* ( X1, Y1, λ1) = ++ λ1(L1-X1-Y1)

Беря частные производные от Т по х1, у1 и λ1 и приравнивая их нулю, получим следующую систему алгебраических уравнений:

,

,

.

Решая эту систему относительно х1 и у1, найдем искомые участки оптимального маршрута

Х1 =, y₁ =L1-,

Отметим три возможных варианта маршрута движения от точки U до P. I_A ( U, C,P ), II_A (U, T, P) для оптимального φ₁ и III_A (UP). С учетом заданных числовых параметров задачи времена движения по этим маршрутам будут равны

t_{A 4} =3.5ч , t_{A 5} = 3.42 , t_{A 6} = 6.02 .

Оптимизация маршрута с города Рязановский до города Королева

Оптимальный маршрут для с города Рязановский до города Королева следует искать на смешанных прямолинейных участках движения. Составляющие маршрута обозначим прямыми N, e, d, D. Оптимизация маршрута означает определение координат z₁ , z , и z₂ , или то же самое, углов φ и η.

По аналогии с предыдущим случаем здесь оптимизируемой функцией является функция вида

а ограничением – линейная функция L= z₁ +z+z_2.

Cучетом их выражений Лангража запишем в следующей форме:

Т^* =

Исследуя эту функцию в том же порядке, что и функцию, окончательно получим:

z₁ =,

z₂ = ,

z= L₁ -

Отметим на карте пять возможных маршрутов выдвижения колонны из точки N в точку DI_в (N,f,e,d,D); II_в ( N,e, d, D); III_в (N, f, c, d); IV_в ( N,e, c, d); V_в (N, D) и для записанных исходных данных вычислим их временные продолжительности. Результаты вычислений представлены следующими значениями t_в1 =5,8 ч, t_в2 = 4,9 ч, t_в3 = 4,95 ч, t_в4 = 4,7 ч, t_в5 =5,97 ч.

Оптимизация маршрута с города Кольчугино до города Королева

Оптимизация маршрута стороны 16 армии означает выбор такого направления движения φ из точки R в точку E (или что тоже самое, выбор координаты Х2), при котором общее время, потребное для совершения маршрута до переправы, было бы минимальным. Из рисунка видно, что маршрут включает два линейных пути, а следовательно, и два интервала времени: время t₁ движения вне дороги на расстояние l = rg и время t₂ движения по дороги на расстояние Y2. Таким образом, Т= t₁ + t₂ .

Но t₁ = = , а t₂ = =