Курсовая работа: Решение задач прогнозирования с помощью статистического пакета SPSS
факторы, формирующие тенденции ряда;
факторы, формирующие циклические колебания ряда;
случайные факторы.
При различных сочетаниях в изучаемом явлении или процессе этих факторов зависимость уровней ряда от времени может принимать различные формы.
Если во временном ряду проявляется длительная тенденция изменения экономического показателя, то говорят, что имеет место тренд.
Если модель является временным рядом, представленным как сумма трендовой, циклической и случайной компонент, то такая модель называется аддитивной моделью временного ряда.
Если в модели временный ряд представлен как произведение перечисленных компонент, то такая модель называется мультипликативной моделью временного ряда.
Для статического анализа одномерных временных рядов экономических показателей вида: y 1 , у2 ,… уn вычисляют ряд величин:
- абсолютный прирост 
, который показывает величину изменения показателя за определенный интервал времени;
- средний абсолютный прирост: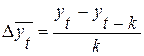 
, т.е. прирост в единицу времени;
- коэффициент роста для t-го периода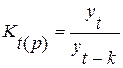 
,
- коэффициент прироста 
.
На практике часто применяют показатель темпа роста и темпа прироста:
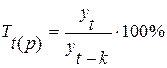, где Т
- темп роста для t -го периода;
, где Т 
- темп прироста для t -го периода.
Предварительный анализ временных рядов экономических показателей заключается в основном в выявлении и устранении аномальных значений уровней ряда, а также в определении наличия тренда в исходном временном ряде. Под аномальным уровнем понимается отдельное значение уровня временного ряда, которое не отвечает потенциальным возможностям исследуемой экономической системы и оказывает существенное влияние на значения основных характеристик временного ряда.
Для выявления аномальных уровней временных рядов используются методы, рассчитанные для статистических совокупностей, например, метод Ирвина предполагает использование следующей формулы:
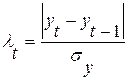; t = 2,3, …, n .
где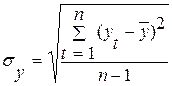 
; 
.
Расчетные значения 
,
и т.д. сравниваются с табличными значениями критерия Ирвина 
, и если какое-то значение оказывается больше табличного, то соответствующее значение у
уровня ряда считается аномальным.
Для определения наличия тренда в исходном временном ряду применяют ряд методов, в частности метод проверки разностей средних уровней.
Чтобы более четко выявить тенденцию развития исследуемого процесса производят сглаживание (выравнивание) временных рядов.
Сглаживания временных рядов можно осуществлять аналитическими или механическими методами.
Суть аналитических методов заключается в построении кривой, проходящей между конкретными уровнями ряда так, чтобы она отображала тенденцию, присущую ряду, и одновременно освобождала его от незначительных колебаний.
Суть методов механического сглаживания заключается в следующем: берется несколько первых уровней временного ряда, образующих интервал сглаживания, и для них подбирается полином, степень которого должна быть меньше числа уровней, входящих в интервал сглаживания; с помощью полинома определяются новые, выровненные значения уровней в середине интервала сглаживания. Далее интервал сглаживания сдвигается на один уровень ряда вправо, вычисляется следующее сглаженное значение и т.д.
Простейшим методом механического сглаживания является метод простой скользящей средней.
При наличии во временном ряду тенденции и циклических изменений значения последующего уровня ряда зависят от предыдущих. Зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней ряда.
Количественно ее можно измерить с помощью индекса корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.
Последовательность коэффициентов автокорреляции уровней первого, второго и т.д. порядков называют автокорреляционной функцией временного ряда (АКФ).