Курсовая работа: Решение задач с нормальными законами в системе "Статистика"
В случае если параметры известны дискриминацию можно провести следующим образом.
Имеются функции плотности 
нормально pacпределенных классов. Задана точка х в пространстве k измерений. Предполагая, что имеет наибольшую плотность, необходимо отнести точку х к i-му классу. Существует доказательство, что если априорные вероятности для определяемых точек каждого класса одинаковы и потери при неправильной классификации i-й группы в качестве j-й не зависят от i и j, то решающая процедура минимизирует ожидаемые потери при неправильной классификации.
Ниже приведен пример оценки параметра многомерногo нормального pacпределения µ и Σ.
µ и Σ мoгyт быть оценены по выборочным данным: 
и 
для классов. Задано l выборок 
из некоторых классов. Математические ожидания 
мoгyт быть оценены средними значениями
(1.2)
Несмещенные оценки элементов ковариационной матрицы Σ есть
(1.3)
Cледовательно, можно определить
и 
по l выборкам в каждом классе при помощи (1.2), (1.3), получив оценки, точку х необходимо отнести к классу, для которой функция f(х) максимальна.
Необходимо ввести предположение, что все классы, среди которых должна проводиться дискриминация, имеют нормальное распределение с одной и той же ковариационной матрицей Σ.
В результате существенно упрощается выражение для дискриминантной функции.
Класс, к которому должна принадлежать точка х, можно определить на
основе неравенства
(1.4)
Необходимо воспользоваться формулой (1.1) для случая, когда их ковариационные матрицы равны:
, а 
( есть вектор математических ожиданий класса i. Тогда (1.4) можно представить неравенством их квадратичных форм
(1.5)
Если имеется два вектора Z и W, то скалярное произведение можно записать 
. В выражении (1.5) необходимо исключить 
справа и слева, поменять у всех членов суммы знаки. Теперь преобразовать
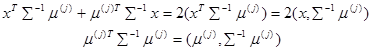
Аналогично проводятся преобразования по индексу i. Необходимо сократить правую и левую часть неравенства (1.5) на 2 и, используя запись квадратичных форм, получается
(1.6)
Необходимо ввести обозначения в выражение (1.6):
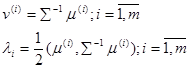
Тогда выражение (1.6) примет вид
(1.7)
Следствие: проверяемая точка х относится к классу i, для которого линейная функция
(1.8)
Преимущество метода линейной дискриминации Фишера заключается в линейности дискриминантной функции (1.8) и надежности оценок ковариационных матриц классов.
Пример
Имеются два класса с параметрами
и 
. По выборкам из этих совокупностей объемом n1 n2 получены оценки 
и 
. Первоначально проверяется гипотеза о том, что ковариационные матрицы 
равны. В случае если оценки и статистически неразличимы, то принимается, что 
и строится общая оценка , основанная на суммарной выборке объемом n1 +n2 , после чего строится линейная дискриминантная функция Фишера (1.8).
2. ДИСКРИМИНАНТНЫЙ АНАЛИЗ ПРИ НОРМАЛЬНОМ ЗАКОНЕ РАСПРЕДЕЛЕНИЯ ПОКАЗАТЕЛЕЙ
Имеются две генеральные совокупности Х и У, имеющие трехмерный нормальный закон распределения с неизвестными, но равными ковариационными матрицами.
Алгоритм выполнения дискриминантного анализа включает основные этапы:
1. Исходные данные представляются либо в табличной форме в виде q подмножеств (обучающих выборок) Mk и подмножества М 0 объектов подлежащих дискриминации, либо сразу в виде матриц X (1) , X (2) , ..., X (q ) , размером (nk ×p ):
Таблица 1
| Номер подмножества Mk (k = 1, 2, ..., q ) | Номер объекта, i (i = 1, 2, ..., nk ) | Свойства (показатель), j (j = 1, 2, ..., p ) | |||
| x 1 | x 2 | … | x 0 | ||
| Подмножество M 1 (k = 1) | 1 |  |  | … |  |
| 2 |  |  | … |  | |
| … | … | … | … | … | |
| n 1 |  |  | … |  | |
| Подмножество M 2 (k = 2) | 1 |  |  | … |  |
| 2 |  |  | … |  | |
| … | … | … | … | … | |
| n 2 |  |  | … |  | |
| … | … | … | … | … | … |
| Подмножество Mq (k = q ) | 1 |  |  | … |  |
| 2 |  |  | … |  | |
| … | … | … | … | … | |
| nq |  |  | … |  | |
| Подмножество M 0 , подлежащее дискриминации | 1 |  |  | … |  |
| 2 |  |  | … |  | |
| … | … | … | … | … | |
| m |  |  | … |  | |
где X (k) - матрицы с обучающими признаками (k = 1, 2, ..., q ),
X (0) матрица новых m -объектов, подлежащих дискриминации (размером m ×p ),
р — количество свойств, которыми характеризуется каждый i -й объект.
Здесь должно выполняться условие: общее количество объектов N множества М должно быть равно сумме количества объектов m (в подмножестве M 0 ), подлежащих дискриминации, и общего количества объектов 
в обучающих подмножествах:
, где q - количество обучающих подмножеств (q ≥2). В реальной практике наиболее часто реализуется случай q =2, поэтому и алгоритм дискриминантного анализа приведен для данного варианта.
2. Определяются 
элементы векторов 
средних значений по каждому j -му признаку для i объектов внутри k -го подмножества (k = 1, 2):
Результаты расчета представляются в виде векторов столбцов:
