Курсовая работа: Решение задачи коммивояжера методом ветвей и границ
![]()
4. Находим степени нулей для приведенной по строкам и столбцам матрицы. Для этого мысленно нули в матице заменяем на знак «∞» и находим сумму минимальных элементов строки и столбца, соответствующих этому нулю. Записываем ее в правом верхнем углу клетки
![]()
5. Выбираем дугу ![]() , для которой степень нулевого элемента достигает максимального значения
, для которой степень нулевого элемента достигает максимального значения
![]()
6. Разбиваем множество всех гамильтоновых контуров ![]() на два подмножества
на два подмножества ![]() и
и ![]() . Подмножество
. Подмножество ![]() гамильтоновых контуров содержит дугу
гамильтоновых контуров содержит дугу ![]() ,
, ![]() - ее не содержит. Для получения матрицы контуров
- ее не содержит. Для получения матрицы контуров ![]() , включающих дугу
, включающих дугу ![]() , вычеркиваем в матрице
, вычеркиваем в матрице ![]() строку
строку ![]() и столбец
и столбец ![]() . Чтобы не допустить образования негамильтонова контура, заменим симметричный элемент
. Чтобы не допустить образования негамильтонова контура, заменим симметричный элемент ![]() на знак «∞».
на знак «∞».
7. Приводим матрицу гамильтоновых контуров ![]() . Пусть
. Пусть ![]() - константа ее приведения. Тогда нижняя граница множества
- константа ее приведения. Тогда нижняя граница множества ![]() определится так
определится так
![]()
8. Находим множество гамильтоновых контуров ![]() , не включающих дугу
, не включающих дугу ![]() . Исключение дуги
. Исключение дуги ![]() достигается заменой элемента
достигается заменой элемента ![]() в матрице
в матрице ![]() на ∞.
на ∞.
9. Делаем приведение матрицы гамильтоновых контуров ![]() . Пусть
. Пусть ![]() - константа ее приведения. Нижняя граница множества
- константа ее приведения. Нижняя граница множества ![]() определится так
определится так
![]()
10. Сравниваем нижние границы подмножества гамильтоновых контуров ![]() и
и ![]() . Если
. Если ![]() , то дальнейшему ветвлению в первую очередь подлежит множество
, то дальнейшему ветвлению в первую очередь подлежит множество ![]() . Если же
. Если же ![]() , то разбиению подлежит множество
, то разбиению подлежит множество ![]() .
.
Процесс разбиения множеств на подмножества сопровождается построением дерева ветвлений.
11. Если в результате ветвлений получаем матрицу ![]() , то определяем полученный ветвлением гамильтонов контур и его длину.
, то определяем полученный ветвлением гамильтонов контур и его длину.
12. Сравниваем длину гамильтонова контура с нижними границами оборванных ветвей. Если длина контура не превышает их нижних границ, то задача решена. В противном случае развиваем ветви подмножеств с нижней границей, меньшей полученного контура, до тех пор, пока не получим маршрут с меньшей длиной или не убедимся, что такого не существует.
3. Математическая модель задачи коммивояжера
Задача коммивояжера может быть сформулирована как целочисленная введением булевых переменных ![]() , если маршрут включает переезд из города i непосредственно в город j и
, если маршрут включает переезд из города i непосредственно в город j и ![]() в противном случае. Тогда можно задать математическую модель задачи, то есть записать целевую функцию и систему ограничений
в противном случае. Тогда можно задать математическую модель задачи, то есть записать целевую функцию и систему ограничений
![]() (1)
(1)
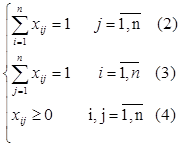
Условия (2) – (4) в совокупности обеспечивают, что каждая переменная ![]() равна или нулю, или единице. При этом ограничения (2), (3) выражают условия, что коммивояжер побывает в каждом городе один раз в него прибыв (ограничение (2)), и один раз из него выехав (ограничение (3)).
равна или нулю, или единице. При этом ограничения (2), (3) выражают условия, что коммивояжер побывает в каждом городе один раз в него прибыв (ограничение (2)), и один раз из него выехав (ограничение (3)).
Однако этих ограничений не достаточно для постановки задачи коммивояжера, так как они не исключают решения, где вместо простого цикла, проходящего через n вершин, отыскиваются 2 и более отдельных цикла (подцикла), проходящего через меньшее число вершин. Поэтому задача, описанная уравнениями (2) – (4) должна быть дополнена ограничениями, обеспечивающими связность искомого цикла.
Для того, чтобы исключить при постановке задачи все возможные подциклы в систему ограничений задачи включают следующее ограничение:
![]() , где
, где ![]() ,
, ![]() и
и ![]() .
.
4. Алгоритм решения
Дана матрица расстояний, представленная в таблице 1. Необходимо с помощью алгоритма Литтла решить задачу коммивояжера.
Табл.1
|
j i | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | ∞ | 7 | 16 | 21 | 2 | 17 |
| 2 | 13 | ∞ | 21 | 15 | 43 | 23 |
| 3 | 25 | 3 | ∞ | 31 | 17 | 9 |
| 4 | 13 | 10 | 27 | ∞ | 33 | 12 |
| 5 | 9 | 2 | 19 | 14 | ∞ | 51 |
| 6 | 42 | 17 | 5 | 9 | 23 | ∞ |
1) Справа к таблице присоединяем столбец Ui , в котором записываем минимальные элементы соответствующих строк. Вычитаем элементы Ui из соответствующих элементов строки матрицы.
|
К-во Просмотров: 374
Бесплатно скачать Курсовая работа: Решение задачи коммивояжера методом ветвей и границ
|