Курсовая работа: Решение задачи коммивояжера методом ветвей и границ

Определим полученный гамильтонов контур. В него вошли дуги

Длина контура равна

Так как границы оборванных ветвей больше длины контура 1 – 5 – 4 – 6 – 3 – 2 – 1, то этот контура имеет наименьшую длину.

алгоритм крускал коммивояжер

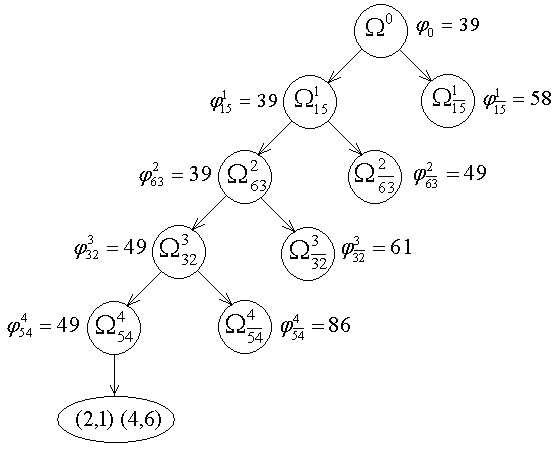
Рис.25

Выводы

Задача коммивояжера является частичным случаем гамильтоновой задачи о путешественнике. Суть задачи коммивояжера состоит в нахождении суммарной минимальной характеристики (расстояния, стоимости проезда и т.д.), при этом коммивояжер должен пройти все n городов по одному разу, вернувшись в тот город, с которого начал.

Существуют несколько методов решения задачи коммивояжера: метод полного перебора, с помощью метода ветвей и границ (алгоритм Литтла), алгоритма Крускала, «деревянного» алгоритма и т.д. Однако только метод ветвей и границ дает нам в итоге самое оптимальное решение.

Основная идея метода Литтла состоит в том, что вначале строят нижнюю границу длин маршрутов для всего множества гамильтоновых контуров . Затем все множество контуров разбивают на два подмножества таким образом, чтобы первое подмножество состояло из гамильтоновых контуров, содержащих некоторую дугу (i,j), а другое подмножество не содержало этой дуги.

Для практической реализации идеи метода ветвей и границ применительно к задаче коммивояжера нужно найти метод определения нижних границ подмножества и разбиения множества гамильтоновых контуров на подмножества (ветвление). Такое определение нижних границ базируется на том утверждении, что если ко всем элементам i-й строки или j-го столбца матрицы C прибавить или отнять число , то задача останется эквивалентной прежней, то есть оптимальность маршрута коммивояжера не изменится, а длина любого гамильтонова контура изменится на данную величину .

Используя ЭВМ, методом ветвей и границ можно решить задачи коммивояжера для .

6. Список использованной литературы

1. О. Е. Акимов «Дискретная математика. Логика, группы, графы», Москва, 2003, 376 с., ил., изд. дом «Лаборатория базовых знаний».

2. Ф. А. Новиков «Дискретная математика для программистов» С.-Петербург, 2002 г. 304 с., ил., изд. дом «Питер».

3. В. М. Бондарев «Основы программирования» 1998 г., 368 с. изд. дом «Феникс»