Курсовая работа: Решение задачи линейного программирования графическим методом

· прибыль от их реализации – согласно условию, соответственно 40 и 20 $.

Таким образом, доход от продажи суточного объема производства радиоприемников первой модели равен $ в сутки, а от продажи радиоприемников второй модели – $ в сутки. Поэтому запишем ЦФ в виде суммы дохода от продажи радиоприемников первой и второй модели:

[$/сутки]

Ограничения

Возможные объемы производства радиоприемников и ограничиваются следующими условиями:

· количество элементов электронных схем, израсходованное в течении суток на производство радиоприемников обоих моделей, не может превышать суточного запаса этих элементов на складе;

· суточный объем первой технологической линии (производство радиоприемников первой модели) не может превышать 60 шт в сутки, второй (производство радиоприемников второй модели) – 80 шт;

· объемы производства радиоприемников не могут быть отрицательными.

Таким образом, все ограничения задачи делятся на 3 группы, обусловленные:

1) расходом элементов электронных схем;

2) суточным объемом технологических линий;

3)неотрицательностью объемов производства.

Запишем эти ограничения в математической форме:

1) Т.к. из условия на радиоприемники первой и второй модели необходимо 15 и 20 элементов соответственно, то данное ограничение имеет вид:

[шт/сутки]

2) Ограничения по суточному объему первой и второй технологических линий имеют вид:

[шт/сутки]

3) Неотрицательность объемов производства задается как

.

Таким образом, математическая модель этой задачи имеет вид

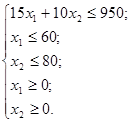
3.3 Нахождение оптимального решения задачи с помощью линейного метода.

Математическую модель задачи о радиоприёмниках мы нашли на предыдущем шаге:

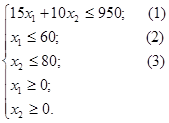
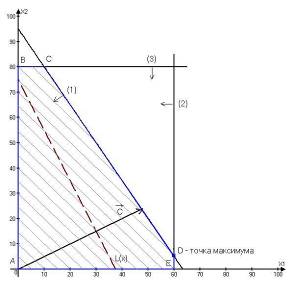
Построим прямые ограничений, для чего вычислим координаты точек пересечения этих прямых с осями координат (рис.3.1).

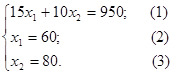
прямая (1) – точки (0;95) и (63,(3);0), прямая (2) проходит через точку параллельно оси , прямая (3) проходит через точку параллельно оси .