Курсовая работа: Решение задачи линейного программирования графическим методом
Определим ОДР. Например, подставим точку (0;0) в исходное ограничение (1), получим ![]() , что является истинным неравенством, поэтому стрелкой обозначим полуплоскость, содержащую точку (0;0), т.е. расположенную правее и ниже прямой (1). Аналогично определим допустимые полуплоскости для остальных ограничений и укажем их стрелками у соответствующих прямых ограничений (см. рис.3.1). Общей областью, разрешенной всеми ограничениями, т.е. ОДР является многоугольник ABCDE.
, что является истинным неравенством, поэтому стрелкой обозначим полуплоскость, содержащую точку (0;0), т.е. расположенную правее и ниже прямой (1). Аналогично определим допустимые полуплоскости для остальных ограничений и укажем их стрелками у соответствующих прямых ограничений (см. рис.3.1). Общей областью, разрешенной всеми ограничениями, т.е. ОДР является многоугольник ABCDE.
Целевую прямую можно построить по уравнению
![]()
Точки пересечения с осями – (0;75) и (37,5;0)
Строим вектор ![]() из точки (0;0) в точку (40;20). Точка D – это последняя вершина многоугольника допустимых решений ABCDE, через которую проходит целевая прямая, двигаясь по направлению вектора
из точки (0;0) в точку (40;20). Точка D – это последняя вершина многоугольника допустимых решений ABCDE, через которую проходит целевая прямая, двигаясь по направлению вектора ![]() . Поэтому D – это точка максимума ЦФ. Определим координаты точки D из системы уравнений прямых ограничений (1) и (2)
. Поэтому D – это точка максимума ЦФ. Определим координаты точки D из системы уравнений прямых ограничений (1) и (2)
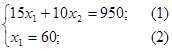
Получили точку D(60;5) [шт/сутки].
Максимальное значение ЦФ равно ![]() [$/сутки].
[$/сутки].
Таким образом, наилучшим режимом работы предприятия является ежесуточное производство радиоприемников первой модели в количестве 60 штук и радиоприемников второй модели в количестве 5 штук. Доход от продажи составит 2500$ в сутки.
4. АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ ОПТИМАЛЬНОГО РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО П РОГРАММИРОВАНИЯ
4.1. Теоретическое введение
Неизбежное колебание значений таких экономических параметров, как цены на продукцию и сырье, запасы сырья, спрос на рынке и т.д. может привести к неоптимальности или непригодности прежнего режима работы. Для учета подобных ситуаций проводится анализ чувствительности, т.е. анализ того, как возможные изменения параметров исходной модели повлияют на полученное ранее оптимальное решение задачи ЛП.
Для решения задач анализа чувствительности ограничения линейной модели классифицируются следующим образом. Связывающие ограничения проходят через оптимальную точку. Несвязывающие ограничения не проходят через оптимальную точку. Аналогично ресурс, представляемый связывающим ограничением, называют дефицитным , а ресурс, представляемый несвязывающим ограничением – недефицитным . Ограничение называют избыточным в том случае, если его исключение не влияет на ОДР и, следовательно, на оптимальное решение. Выделяют следующие три задачи анализа на чувствительность.
1. Анализ сокращения или увеличения ресурсов :
· на сколько можно увеличить (ограничения типа ![]() ) запас дефицитного ресурса для улучшения оптимального значения ЦФ?
) запас дефицитного ресурса для улучшения оптимального значения ЦФ?
· на сколько можно уменьшить (ограничения типа ![]() ) запас недефицитного ресурса при сохранении оптимального значения ЦФ?
) запас недефицитного ресурса при сохранении оптимального значения ЦФ?
2. Увеличение (ограничения типа ![]() ) запаса какого из ресурсов наиболее выгодно ?
) запаса какого из ресурсов наиболее выгодно ?
3. Анализ изменения коэффициентов ЦФ : каков диапазон изменения коэффициентов ЦФ, при котором не меняется оптимальное решение?
4.2. Методика графического анализа чувствительности оптимального решения .
4.2.1. Первая задача анализа на чувствительность (анализ на чувствительность к правой части ограничений)
Проанализируем чувствительность оптимального решения задачи о производстве радиоприемников. ОДР задачи (рис.3.1) – многоугольник ABCDE. В оптимальной точке D пересекаются прямые (1) и (2). Поэтому ограничения (1) и (2) являются связывающими , а соответствующие им ресурсы (суточный объем элементов электронных схем и производительность первой технологической линии) – дефицитными .
Рассмотрим экономический смысл этих понятий. Точка максимума ЦФ D соответствует суточному производству 60 шт радиоприемников первой модели и 5 шт радиоприемников второй модели. В производстве радиоприемников используются однотипные элементы электронных схем. Суточный запас на складе этих элементов – это правая часть связывающего ограничения (1) (950 шт/сутки). Согласно этому ограничению, на производство в точке D расходуется
![]() [шт элементов/сутки](1).
[шт элементов/сутки](1).
Аналогично видим, что производительность первой технологической линии - это правая часть связывающего ограничения (2) (60 шт/сутки). Согласно этому ограничению в точке D данная линия производит 60 радиоприемников первой модели в сутки.
Таким образом, понятие "связывающие ограничения " (1) и (2) означает, что при производстве радиоприемников в точке D(60;5) запасы элементов электронных схем расходуются полностью, а так же производительность первой технологической линии используется в полном объеме. По этой причине невозможно дальнейшее наращивание производства. В этом заключается экономический смысл понятия дефицитности ресурсов, т.е. если предприятие сможет увеличить суточные запасы элементов электронных схем или производительность первой технологической линии, то это позволит увеличить выпуск радиоприемников. В связи с этим возникает вопрос: до какого уровня целесообразно увеличить данные ресурсы, и на сколько при этом увеличится оптимальное производство радиоприемников?
Правило №1
Чтобы графически определить максимальное увеличение запаса дефицитного ресурса, вызывающее улучшение оптимального решения,
необходимо передвигать соответствующую прямую в направлении улучшения ЦФ до тех пор, пока это ограничение не станет избыточным .
При прохождении прямой (1) через точку К (рис.4.1) многоугольник ABKE становится ОДР, а ограничение (1) – избыточным. Действительно, если удалить прямую (1), проходящую через точку К, то ОДР ABKE не изменится. Точка К становится оптимальной , в этой точке ограничения (2) и (3) становятся связывающими.
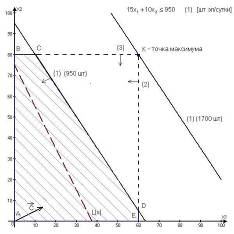
Рис.4.1. Анализ увеличения суточного запаса элементов электронных схем
Правило №2