Курсовая работа: Розробка операційного та керуючого автомату що виконує операцію прискореного множення
Вступ
У наш час, з розвитком науково-технічного прогресу розвивається і обчислювальна техніка, що сприяє більшому удосконаленню. Обчислювальна техніка займає не останнє місце і грає визначальну роль в науковому технічному прогресі, сприяє підвищенню ефективності виробництва, покращанню якості продукції, росту продуктивності праці.
ЕОМ відкрили нову сторінку в історії людських знань і можливостей, звільнили тисячі обчислювачів, значно полегшили працю вчених, дали можливість вивчати найскладніші процеси.
В основу проектування операційних пристроїв різноманітного призначення покладено принцип функціонування мікропрограмування. Пристрої проектуються, як композиція операційного і керуючого автоматів. Мікропрограмування – це спосіб опису функцій операційних пристроїв незалежно від технічних засобів, які використовуються для їх реалізації. Таке тлумачення мікропрограми дозволяє синтезувати структуру будь-яких операційних пристроїв незалежно від способу керування роботою пристрою.
Необхідно відмітити, що принципи побудови і методи проектування операційних і керуючих автоматів є тією основою, на якій базується теорія і практика проектування більшої частини пристроїв ЕОМ.
1. Розробка операційного автомату
1.1 Метод виконання операції прискореного множення
В даній курсовій роботі розглядається операція прискореного множення в доповняльному коді, зі старших розрядів.
Стосовно двійкової системи числення найбільш відомі наступні основні способи виконання операції множення: множення, починаючи з молодших розрядів множника; множення, починаючи з старших розрядів множника.
В обох випадках операція множення складається з ряду послідовних операцій додавання часткових добутків. Операціями додавання керують розряди множника: якщо в деякому розряді множника знаходиться одиниця, то до суми часткових добутків додається множене з відповідним зсувом, якщо в розряді множника – нуль, то множене не додається.
Якщо розрядність чисел значна то процес множення може потребувати значного часу, тому існують різні методи прискорення операції множення. Зокрема існують такі методи:
![]()
![]() 1) Прискорення за рахунок заміни комбінацій цифр. Наприклад: комбінації 00, 01 і 10 не перетворюються, а комбінація 11 замінюється на 01 і 1 йде в наступний розряд. При виконані множення, якщо в деякому розряді множника знаходиться 1, то до суми часткових добутків додається множене з відповідним зсувом, а якщо 1, то до суми часткових добутків додається доповняльний код множеного з відповідним зсувом.
1) Прискорення за рахунок заміни комбінацій цифр. Наприклад: комбінації 00, 01 і 10 не перетворюються, а комбінація 11 замінюється на 01 і 1 йде в наступний розряд. При виконані множення, якщо в деякому розряді множника знаходиться 1, то до суми часткових добутків додається множене з відповідним зсувом, а якщо 1, то до суми часткових добутків додається доповняльний код множеного з відповідним зсувом.
2) Множення з запам’ятовуванням переносів: додаються три часткові добутки без розповсюдження переносу і формується проміжна сума і проміжний перенос; додаються без розповсюдження переносу проміжну суму, проміжний перенос та наступний частковий добуток, формується чергова проміжна сума і проміжний перенос; аналогічні дії виконуються до тих пір, поки не виконається додавання останнього часткового добутку; останній крок додавання з розповсюдженням переносу проміжної суми та проміжного переносу.
3) Прискорення множення при поділенні множника на дві частини: якщо множник має парну кількість розрядів, його ділять на дві рівні частини, відбувається множення множеного на число в два разу меншої розрядності ніж у В, отриманні добутки додаються з врахуванням зсуву.
В даній курсовій роботі будемо використовувати метод множення з запам’ятовуванням переносів, розглянемо його більш детально:
Множимо числа з фіксованою комою в доповняльному коді. Множення виконується з врахуванням знакового розряду, якщо В>0 то виконуємо множення, якщо В<0 то робимо корегуючі дії: додаємо доповнений код числа А. Додаємо також ще два часткові добутки (з врахуванням зсуву) без розповсюдження переносу і формуємо проміжну суму і проміжний перенос.
Потім додаємо без розповсюдження переносу проміжну суму, проміжний перенос та наступний частковий добуток (з врахуванням зсуву) і формуємо чергову проміжну суму і проміжний перенос. Ці дії виконуємо до тих пір, поки не додамо останній частковий добуток.
Останній крок: додавання з розповсюдженням переносу проміжної суми та проміжного переносу.
Отриманий результат теж буде в доповняльному коді, тому дивимося на знак результату: якщо результат додатній, то його прямий код співпадає з оберненим і не потрібно переводити, якщо ж результат від’ємний, то доповняльний код необхідно перевести у прямий, для цього інвертуємо результат і додаємо до нього одиницю, отримаємо прямий код результату.
1.2 Розробка алгоритму
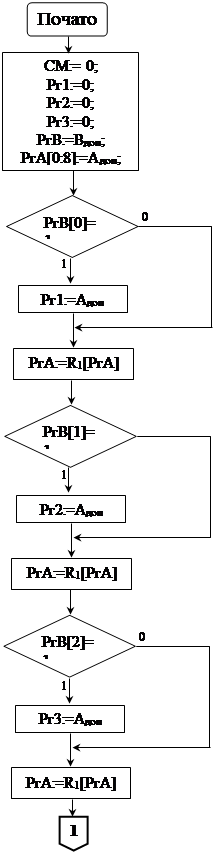
Згідно обраного методу виконання множення побудуємо блок схему алгоритму:
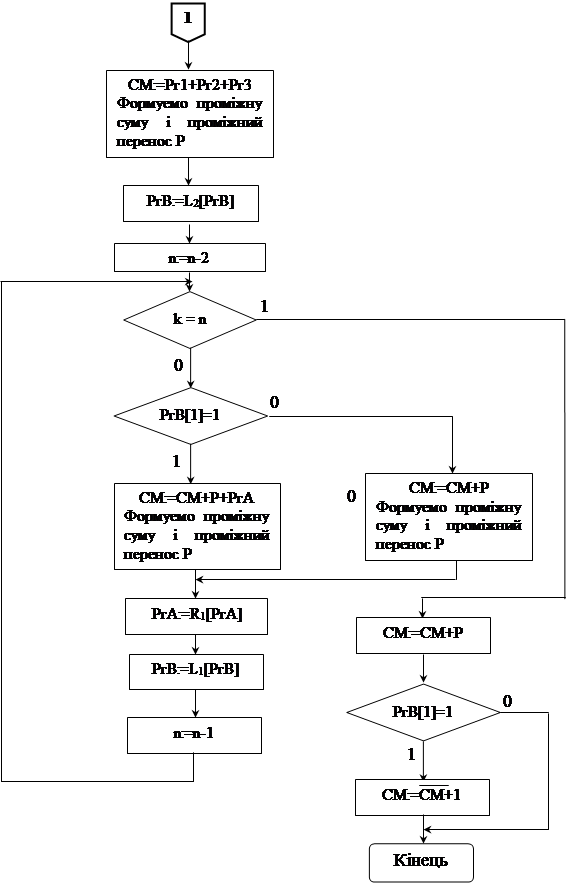
Описання блок-схеми алгоритму
Спочатку виконуємо ініціалізацію:
- в суматор заносимо 0;
- в регістр Рг1 заносимо 0;
- в регістр Рг2 заносимо 0;
- в регістр Рг3 заносимо 0;
- в лічильник n заносимо 8;
- у перші 8 розрядів регістра РгА заносимо доповняльний код числа А;
- в регістр РгВ заносимо доповняльний код числа В;
--> ЧИТАТЬ ПОЛНОСТЬЮ <--