Курсовая работа: Розвязання задачі Коші для звичайного диференціального рівняння першого порядку методом Ейлера
При цьому допускається похибка : ![]() . Далі використовується точка, яку можна вважати початковою
. Далі використовується точка, яку можна вважати початковою ![]() і за допомогою її визначається наступна точка
і за допомогою її визначається наступна точка ![]() і так далі.
і так далі.
Отже узагальнена формула методу Ейлера набуває вигляду:
![]()
Похибка, що допускається на кожному кроці : ![]() . Сума всіх похибок при обчисленні на кожному з кроків вирішення дає нам загальну похибку
. Сума всіх похибок при обчисленні на кожному з кроків вирішення дає нам загальну похибку ![]() . Метод Ейлера є аналогом методу прямокутників для чисельного інтегрування. Якщо права частина початкового ДР* не залежить від у, то значення шуканої функції в точці
. Метод Ейлера є аналогом методу прямокутників для чисельного інтегрування. Якщо права частина початкового ДР* не залежить від у, то значення шуканої функції в точці ![]() визначається інтегралом
визначається інтегралом ![]() і тоді загальна формула методу Ейлера являє собою формулу лівих прямокутників. Але, на відміну від інтегрування, де похибки просто сумувалися, при вирішенні ДР похибка на попередньому кроці веде до ще більшої похибки на наступному кроці, і як правило сумарна похибка зростає експоненціально з кількістю пройдених вже кроків.
і тоді загальна формула методу Ейлера являє собою формулу лівих прямокутників. Але, на відміну від інтегрування, де похибки просто сумувалися, при вирішенні ДР похибка на попередньому кроці веде до ще більшої похибки на наступному кроці, і як правило сумарна похибка зростає експоненціально з кількістю пройдених вже кроків. ![]() . Тож використовуємо модифікований метод Ейлера як найбільш точний.
. Тож використовуємо модифікований метод Ейлера як найбільш точний.
Похибка при вирішенні задачі Коші для звичайних диференціальних рівнянь першого порядку методом Ейлера
Для ЗДР першого порядку ![]() що має ПУ
що має ПУ ![]() загальна формула методу Ейлера має вигляд
загальна формула методу Ейлера має вигляд ![]() . Якщо позначити дійсне вирішення задачі Коші як
. Якщо позначити дійсне вирішення задачі Коші як ![]() , то похибка Е в вузлі
, то похибка Е в вузлі ![]() може бути представлена у вигляді
може бути представлена у вигляді
![]() .
.
Кали ми визначаємо приріст функції
![]()
та вводимо умовні позначення
![]() ,
,
то можливо оцінити ![]() зверху :
зверху :
 .
.
Якщо припустити, що початкова похибка рівна нулю, то випливає висновок :
 .
.
Тепер, якщо замінити ![]() у границі
у границі ![]() , отримаємо:
, отримаємо:
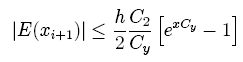 .
.
З останнього співвідношення видно, що при ![]() похибка Е зростає експоненціально з координатою (при
похибка Е зростає експоненціально з координатою (при![]() отримуємо
отримуємо ![]() ).
).
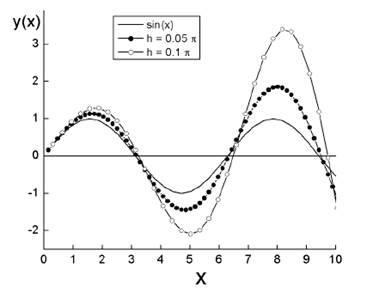
Мал. 1
На мал.1 приведені підрахунки для рівняння ![]() (вирішення -
(вирішення - ![]() ). Єдиний спосіб оцінити масштаби похибки, що наросла – провести декілька пробних підрахунків з різними кроками по х.
). Єдиний спосіб оцінити масштаби похибки, що наросла – провести декілька пробних підрахунків з різними кроками по х.
Алгоритм розв’язання диференціального рівняння першого порядку методом Ейлера
Нижче поданий алгоритм чисельно інтегрує звичайне диференціальне рівняння першого, другого та третього порядку з використанням модифікованого прямого методу Ейлера
При чисельному інтегруванні диференціального рівняння першого порядку y' = F(x,y)
З початковою умовою y(x0 ) = y0 (задача Коші) спочатку вибираємо
порядок похідної – у нашому випадку згідно з варіантом курсової – порядок 1 (диференціальне рівняння першого порядку). Далі визначаємо коефіцієнти та коефіцієнт при х. Вводимо границі відрізку . Фіксований приріст аргументу h = (xf -x0 )/n, де xf - кінцева точка інтервалу інтегрування , n – кількість кроків. Потім, використовуючи процедуру модифікованого методу Ейлера, , обчислюємо yk згідно з рекурсивною формулою:
yk = yk-1 +h[Fk-1 +F(xk , yk-1 +hFk-1 )]/2