Курсовая работа: Сечение многогранников
Метод построения сечения заключается в нахождении точек пересечения секущей плоскости с гранями многогранника, а вернее с ребрами многогранника. Проверка на пересечение секущей плоскости и ребра многогранника производится следующим образом:
1. Составление уравнения секущей плоскости по трем точкам;
2. Подстановка в уравнение координат концов ребра с целью проверки: расположены ли точки в разных полупространствах относительно плоскости сечения.
3. Нахождение точки пересечения ребра многогранника и плоскости сечения.
Для каждой грани записываются две точки, причем запись производится только для тех граней, где плоскость сечения пересекла два ребра. Далее используя полученные данные, строится многоугольник сечения следующим образом:
1. Берем первую пару точек и ищем следующую пару точек в которой повторяется одна из точек первой пары.
2. Найдя следующую пару проделываем для нее тоже самое, что и для первой пары, но исключаем из поиска первую пару.
3. Проделываем весь алгоритм для каждой пары, пока не останется одна ненайденная точка.
4. Полученная цепочка является последовательным описанием ребер многоугольника сечения.
Далее запоминаем полученный многоугольник, как новую грань многогранника.
2.4 Исследование свойств сечения
Перечислим некоторые свойства сечения (исходя из факта, что сечением является многоугольник).
1. Уравнение плоскости сечения.
2. Количество вершин многоугольника сечения.
3. Площадь многоугольника сечения.
4. Координаты вершин многоугольника сечения.
5. Двугранный угол между плоскостью сечения и гранями многогранника.
6. Углы при вершинах многоугольника сечения.
Некоторые из этих свойств реализованы в программе (1,2,3,4).
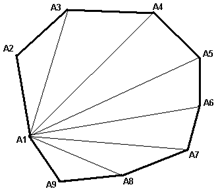
Пример: Нахождение площади сечения. Так как строятся сечения выпуклых многогранников, то многоугольник сечения будет тоже выпуклым, т.е. его площадь можно найти разбиением на треугольники (площадь сечения равна сумме площадей треугольников из которых оно составлено).
Глава III. Визуализация
3.1 Способы визуализации трехмерного пространства
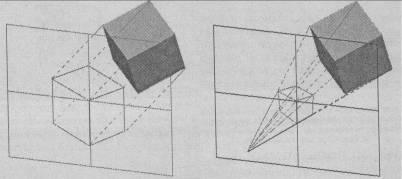
Для визуализации используются два вида проекций: параллельные (аксонометрические) (на рисунке слева) и центральные (перспективные)
(на рисунке справа). При построении аксонометрической проекции пространственного тела его отдельные точки сносятся на плоскость проекции параллельным пучком лучей, а при построении центральной проекции – пучком лучей исходящих из одной точки, соответствующей положению глаз наблюдателя. Частным случаем аксонометрической проекции является проекция ортографическая, при построении которой плоскость проекции выравнивается параллельно одной из координатных плоскостей.
3.2 Перекрытие
Под перекрытием понимается тот факт, что невозможно одновременно видеть все грани многогранника и какие - то грани обязательно окажутся невидимыми. Проблема состоит в том, как узнать какие грани видны, а какие нет. В проекте мы рассматриваем только выпуклые многогранники, поэтому для реализации перекрытия используется тот факт, что нормальный вектор к каждой грани направлен извне. Т.е. если использовать ортографическую проекцию, то тот факт, что координатная составляющая (оси проекции) нормального вектора положительна, то грань видима, если отрицательна, то грань перекрыта.
