Курсовая работа: Синтезування логічної структури пристрою у базісі АБО–НІ
Пояснювальна записка
Зміст
1. Вступ
2. Мінімізація логічної функції методом Квайна
3. Мінімізація логічної функції методом карт Карно (Вейча)
4. Синтез структури у заданому базисі
5. Висновок
6. Список літератури
Вступ
В сучасному світі такий пристрій як ЕОМ застосовується практично всюди, в науці, в навчанні, в економіці, у військовій галузі і т.д. Це зумовлено тим що ЕОМ може обробляти інформацію дуже і дуже швидко.
Цифрові ЕОМ працюють з інформацією, представленою в дискретній формі у вигляді загальноприйнятої для запису та читання символіки набором цифр, букв та знаків будь-якого установленого алфавіту, який має кінцеве число символів.
Основна мета курсового проекту – надбання практичних та закріплення теоретичних навичок в розробці апаратних засобів логічних пристроїв різноманітного призначення.
В завданні требасинтезувати логічну структуру пристрою у базісі АБО-НІ.
Для формального опису цифрового автомату (блоки ЕОМ представляють собою цифрові автомати) використовують апарат алгебри логіки). У загальному випадку логічні вирази є функціями логічних змінних A, B, C,… що, як i їх логічні змінні, можуть приймати тільки два значення 0 або 1. Структурна схема логічного пристрою може бути побудована безпосередньо за канонічною формою (ДКНФ) функції, що реалізується. Недоліком такого методу побудування структурних схем, що забезпечують правильне функціонування пристрою, є те, що отримані схеми, як правило, виходять невиправдано складними, потребують великої кількості логічних елементів i, відповідно, мають низьку економічність i надійність. У багатьох випадках вдається так спростити логічний вираз, не порушуючи функції, що відповідна структурна схема виходить істотно простішою. Методи такого спрощення функції називають методами мінімізації логічних функцій.
1. Перший етап
1.1 Мінімізація логічних функцій методом Квайна
Метод Квайна відноситься до числа таких методів мінімізації функцій алгебри логіки, які дозволяють зображати функції в КНФ з мінімальним числом членів i мінімальним числом літер у членах. Цей метод має два етапи перетворення функції: на першому етапі здійснюється перехід від канонічної форми (ДКНФ) до, так званої, СКОРОЧЕНОЇ ФОРМИ, а на другому етапі – перехід від скороченої форми логічного виразу до МIНIМАЛЬНОЇ ФОРМИ.
1.2 Нехай функція задана таблицею істинності (табл. 1)
Таблиця 1
| A | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| B | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| C | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| D | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| F (A, B, C, D) | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
ДКНФ даної функції:
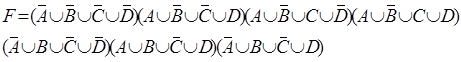 (1)
(1)
Метод Квайна працює лише для ДДНФ. Щоб отримати її потрібно зробити інверсію даної функції:
![]() (2)
(2)
Перехід до скороченої форми складається з послідовного використання двох операцій: операції склеювання та операції поглинання.
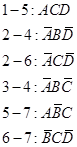
Вираз, який отримали, є скороченою формою логічного виразу заданої функції, а його члени – прості імпліканти функції.
![]() (3)
(3)
2. Другий етап
Перехід від скороченої форми до мінімальної здійснюється за допомогою iмплiкантної матриці (табл. 2). У стовпчики iмплiкантної матриці записуються члени ДДНФ заданої функції, а в рядки – прості імпліканти функції, тобто члени скороченої форми логічного виразу функції. У матриці помічаються (наприклад, хрестиками) стовпчики членів ДДНФ, що поглинаються окремими простими iмплiкантами.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--