Курсовая работа: Система автоматического регулирования

Рассмотрим возможность ПИ-закона регулирования САР температуры. Для этого построим структурную схему, в которую включим ПИ-регулятор.

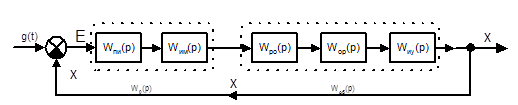
Рис 10. Структурная схема САР температуры.

Передаточная функция ПИ-регулятора имеет вид

W_P (р)=К+1/Т_р ; (К=20; Т_и =25 сек.)

Найдем передаточную функцию разомкнутой системы

W_раз (р)=W_р (р)W_об (р)

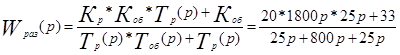
Найдем передаточную функцию замкнутой системы

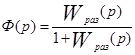
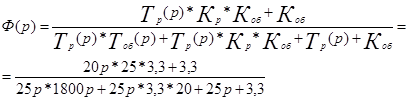
По передаточной функции разомкнутой системы строим ЛАЧХ и ЛФЧХ, а по функции замкнутой системы строим АФХ.

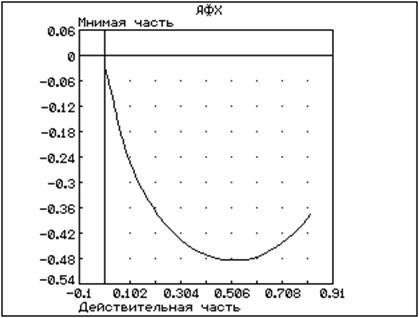
Рис 11. Амплитудно-фазовая характеристика замкнутой системы.

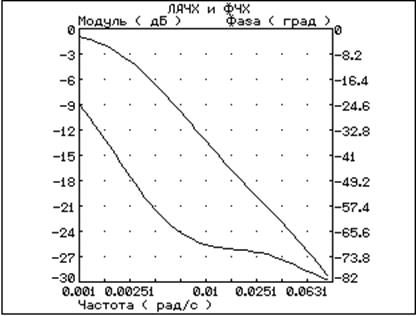
Рис 12. ЛАЧХ и ЛФЧХ при астатическом регулировании.

Частотные характеристики показывают, что система имеет запас устойчивости, как по амплитуде, так и по фазе, т.к. на частоте среза w_ср фаза < 180° значит возможно использовать ПИ регулятор для САР температуры.

2.1.3. Исследование качества одноконтурной САР.

К автоматическим системам регулирования предъявляются требования не только в отношении ее устойчивости. Для работоспособности системы не менее необходимо, что бы процесс автоматического регулирования при определенных качественных показателей.

Требования к качеству процесса регулирования в каждом случае могут быть самыми разнообразными, однако из всех качественных показателей можно выделить несколько наиболее существенных, которые с достаточной полнотой определяют качество почти всех АСР.

Качество процесса регулирования системы, как правило, оценивают по ее переходной функции.

Основными показателями качества является: - время регулирования t_р – называется время, в течении которого, начиная с момента приложения воздействия на систему отклонения регулируемой величины Dh(t) от ее установившегося значения h₀ =h(¥) будут меньше на пред заданной величины Е. Обычно принимают, что по истечении времени регулирования отклонении регулируемой величины от установившегося значения должно быть не более Е=5%. Таким образом, время регулирования определяет длительность (быстродействие) переходного процесса.

- перерегулированием s называется максимальное отклонение Dh_max регулируемой величины от установившегося значения, выраженное в процентах от h₀ =h(¥).

Абсолютная величина Dh_max определяется из кривой переходного процесса:

Dh_max =h_max - h(¥)

Соответственно перерегулирование будет равно:

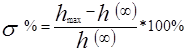
- Колебательность системы характеризуется числом колебаний регулируемой величины за время регулирования t_р . Если за это время переходный процесс в системе совершает число колебаний меньше заданного, то считается, что система имеет требуемые качеством регулирования в части ее колебательности;

- Установившаяся ошибка Е. Установившееся значение регулируемой величины h₀ в окончании переходного процесса зависит от астатизма n системы. В статических системах (n=0) – установившаяся ошибка при постоянной величине входного воздействия не равна 0 и следовательно, установившееся значение регулируемой величины h₀ будет отличаться от ее заданного значения на величину установившейся ошибки.