Курсовая работа: Система массового обслуживания с ограниченным временем ожидания

Отсюда:

.

Пример 1. Автозаправочная станция (АЗС) представляет собой СМО с одним каналом обслуживания (одной колонкой).

Площадка при станции допускает пребывание в очереди на заправку не более трех машин одновременно (m = 3). Если в очереди уже находятся три машины, очередная машина, прибывшая к станции, в очередь не становится. Поток машин, прибывающих для заправки, имеет интенсивность =1 (машина в минуту). Процесс заправки продолжается в среднем 1,25 мин.

Определить:

вероятность отказа;

относительную и абсолютную пропускную способности АЗС;

среднее число машин, ожидающих заправки;

среднее число машин, находящихся на АЗС (включая обслуживаемую);

среднее время ожидания машины в очереди;

среднее время пребывания машины на АЗС (включая обслуживание).

Иначе говоря, среднее время ожидания равно среднему числу заявок в очереди, деленному на интенсивность потока заявок.

Находим вначале приведенную интенсивность потока заявок: =1/1,25=0,8; =1/0,8=1,25.

По формулам (8):

Вероятность отказа 0,297.

Относительная пропускная способность СМО: q=1-=0,703.

Абсолютная пропускная способность СМО: A==0,703 машины в мин.

Среднее число машин в очереди находим по формуле (12):

,

т.е. среднее число машин, ожидающих в очереди на заправку, равно 1,56.

Прибавляя к этой величине среднее число машин, находящихся под обслуживанием:

получаем среднее число машин, связанных с АЗС.

Среднее время ожидания машины в очереди по формуле (15):

Прибавляя к этой величине , получим среднее время, которое машина проводит на АЗС:

Системы с неограниченным ожиданием. В таких системах значение т не ограничено и, следовательно, основные характеристики могут быть получены путем предельного перехода в ранее полученных выражениях (5), (6) и т.п.

Заметим, что при этом знаменатель в последней формуле (6) представляет собой сумму бесконечного числа членов геометрической прогрессии. Эта сумма сходится, когда прогрессия бесконечно убывающая, т.е. при <1.

Может быть доказано, что <1 есть условие, при котором в СМО с ожиданием существует предельный установившийся режим, иначе такого режима не существует, и очередь при будет неограниченно возрастать. Поэтому в дальнейшем здесь предполагается, что <1.

Если, то соотношения (8) принимают вид:

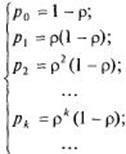(16).

При отсутствии ограничений по длине очереди каждая заявка, пришедшая в систему, будет обслужена, поэтому q=1, .