Курсовая работа: Совокупный спрос на рынке благ
При заданных Пi величина суммы их дисконтированных значений зависит от величины R . То значение R , которое превращает неравенство (5) в равенство, называется предельной эффективностью капитала (R*).
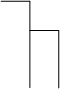
Когда инвестор имеет возможность выбирать между несколькими вариантами инвестирования, он остановится на тех из них, у которых R* самая большая. Почему? Это легко понять, если R* рассматривать в качестве ставки ссудного процента, при которой инвестиционный проект можно осуществить за счет заёмных средств и “остаться при своих”, т.е. полностью возвратить кредит с процентами из ожидаемых доходов. Очевидно, что те кредиты лучше, которые “окупаются” при более высокой ставке ссудного процента. Расположим все существующие инвестиционные проекты по мере убывания их предельной эффективности, как это представлено на рис.10.

![]() R *
R *

![]() i 2
i 2
![]() i1
i1
![]()
I II III IV V I
Рис.10 Ранжирование инвестиционных проектов по их предельной эффективности.
Тогда объём рационального инвестирования можно представить как убывающую функцию от предельной эффективности капитала: I=I(R*) . Эту функцию не следует интерпретировать таким образом, что объём инвестиций возрастает по мере снижения R* . Речь идет лишь о том, что при наличии разноэффективных вариантов капиталовложений инвестиционные средства целесообразно распределять на основе ранжирования вариантов по их R* .
Кроме доходности вариантов капиталовложений инвестор должен учитывать степень риска каждого из них. Среди всех вариантов вложений есть один самый надежный - это покупка государственных облигаций. По ним всегда в срок выплачиваются установленные проценты. Поэтому ставку процента по государственным облигациям можно рассматривать в качестве нижнего предела R* для вложений в реальный капитал. При ставке i 1 инвестиции будут сделаны в первые четыре варианта из представленных на рис.10. Если же ставка процента возрастет до i 2 , то реализуются лишь два первых проекта. В реальный капитал делаются вложения, если R*> i . При заданной функции I (R*) объем инвестиций в производство тем больше, чем ниже i . Следовательно, функцию автономных инвестиций можно представить формулой: I a = I i ( R* - i ),
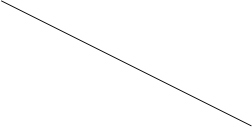
где Ii - предельная склонность к инвестированию, которая показывает, на сколько единиц увеличатся инвестиции в случае снижения ставки процента на один пункт . Так выводится кейнсианская функция автономных инвестиций. Ее график изображен на рис. 11.
![]() i
i
![]()
![]()
![]()
![]()
 R *
R *
a
R * - i
![]()
![]()
![]()
![]() D i{
D i{
![]()
![]() I
I
DI
Рис.11 График функции автономных инвестиций.
Другая цепь логических рассуждений используется неоклассиками.
Предприниматели прибегают к инвестициям для того, чтобы довести объём имеющегося у них капитала до оптимальных размеров. Зависимость объёма инвестиций от размера функционирующего капитала можно представить формулой
I a t =b ( K* - K t ); 0<b <1; (6)
где I a t - объем автономных инвестиций в период t; K t - объём капитала существующий на начало периода t; K*- оптимальный объём капитала, b - коэффициент, характеризующий меру приближения существующего объёма капитала к оптимальному за период t .
Оптимальным является такой размер капитала, который при существующей технологии обеспечивает максимальную прибыль. Из микроэкономики известно, что прибыль достигает максимума, когда предельная производительность капитала (r ) равна предельным затратам его использования. В условиях совершенной конкуренции предельные затраты использования капитала слагаются из нормы амортизации (d ), определяющей величину износа капитала, и ставки процента по финансовым активам (i ), представляющей альтернативные затраты использования средств в качестве капитала. Следовательно, прибыль максимальна при r = d + i .
Пусть технология производства характеризуется производственной функцией Кобба - Дугласа: