Курсовая работа: Создание функциональной модели вычисления минимума заданной функции методом парабол

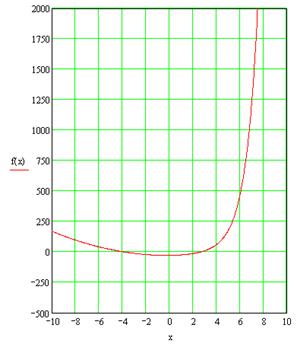
Рисунок 1. Функция

Пример 2. Найти минимум функции методом парабол на промежутке [-2; -1] с требуемой точностью 0,0001.

Решение:

k номер итерации
1	-1,882843	0,831300
2	-1,919519	-0,009568
3	-1,919112	-0,000004

Таблица 2. Пример 2

Так как < , следовательно минимум x = -1,919112.

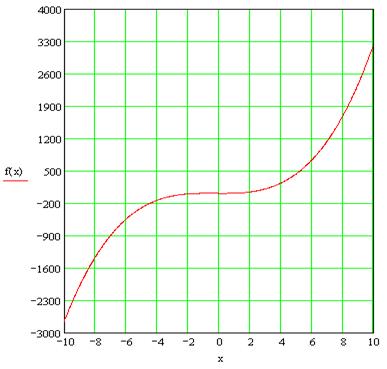
Рисунок 2. Функция

Пример 3. Найти минимум функции методом парабол на промежутке [-1; -0,5] с требуемой точностью 0,00001.

Решение:

k номер итерации
1	-0,497419	0,116021
2	-0,451529	-0,003278
3	-0,450185	-0,000003

Таблица 3. Пример 3

Так как < , следовательно минимум x = -0,450185.

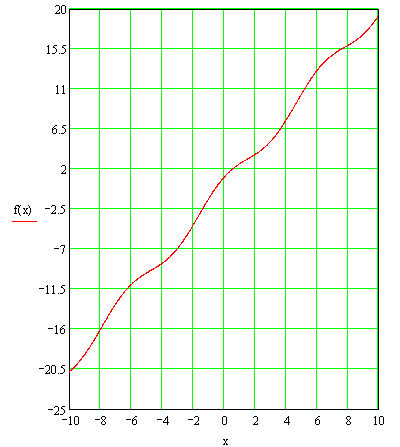
Рисунок 3. Функция

2 Математические и алгоритмические основы решения задачи

Пусть имеет первую и вторую производную. Разложим в ряд Тейлора в некоторой точке , ограничиваясь при этом тремя членами разложения:

. (3)

Иными словами, аппроксимируем нашу функцию в точке , параболой (рисунок 1). Для этой параболы можно аналитически вычислить положение экстремума как корень уравнения первой производной от (3):

.

Пусть минимум аппроксимирующей параболы находится в точке . Тогда вычислив значение функции , мы получаем новую точку приближения к минимуму.

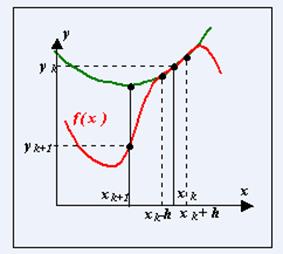
Рисунок 4. Поиск минимума функции методом парабол

Обычно в практических реализациях данного метода не используют аналитический вид первой и второй производных . Их заменяют конечно-разностными аппроксимациями. Наиболее часто берут симметричные разности с постоянным шагом h:

Это эквивалентно аппроксимации функции параболой, проходящей через три близкие точки

, , .

Окончательное выражение, по которому можно строить итерационный процесс, таково:

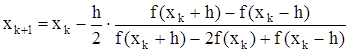(4)