Курсовая работа: Создание функциональной модели вычисления минимума заданной функции методом парабол

1) знаменатель формулы

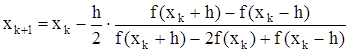
должен быть > 0. Если это не так, нужно сделать шаг в обратном направлении, причем достаточно большой. Обычно в итерационном процессе полагают

.

Иногда ради упрощения расчетов полагают

,

однако это существенно уменьшает скорость сходимости.

2) если это не так, то от следует сделать шаг

,

с .

Если и при этом условие убывания не выполнено, уменьшают τ и вновь делают шаг.

3 Функциональные модели и блок-схемы решения задачи

Функциональные модели и блок-схемы решения задачи представлены на рисунке 5, 6.

Используемые обозначения:

·X0, MIN_VAL – начальная точка;

·H, MAX_VAL – конечная точка;

·EPS – требуемая точность;

·FN – функция для вычисления минимума;

·X1 – вспомогательная точка;

·X2 – вспомогательная точка;

·XN – вспомогательная точка;

·F_X0 – функция от начальной точки X0;

·F_X1 – функция от вспомогательной точки X1;

·F_X2 – функция от вспомогательной точки X2;

·F_XN – функция от вспомогательной точки XN;

·Q – рабочая переменная;

·A – рабочая переменная;

·B – рабочая переменная;

·C – рабочая переменная;