Курсовая работа: Спеціальні класи та функціональна повнота системи функцій алгебри логіки. Теорема Поста

Оскільки, а, серед наборів знайдуться два сусідні і, такі що і. Нехай вони відрізняються в r-му розряді: ,. Тоді визначимо функцію так: . Справді, тоді, і. Лема доведена.

Лема 4(про нелінійну функцію.) [1, ст. 11]. З будь-якої нелінійної функції алгебри логіки , підставляючи замість усіх змінних, можна отримати або .

Доведення. Нехай. Розглянемо поліном Жегалкіна цієї функції.

З її нелінійності випливає, що в ньому присутні складові виду. Будемо вважати, що існує добуток . Таким чином, поліном Жегалкіна цієї функції виглядає так

,

Причому

Інакше кажучи, такі, що.

Розглянемо допоміжну функцію

.

Тоді функція

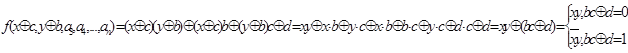
Лему доведено.

Теорема 11

Cистема функцій алгебри логіки є повною в тоді і тільки тоді, коли вона не міститься цілком в жодному із класів: .

Доведення

Необхідність. Нехай – повна система, – будь-який з класів і нехай

Тоді

Отримане протиріччя завершує обґрунтування необхідності.

Достатність. Нехай

Тоді в існують функції

Достатньо показати, що

Розіб’ємо доведення на три частини: отримання заперечення, констант і кон’юнкції.

1. Отримання . Розглянемо функцію і введемо функцію . Так як функція не зберігає 0, . Можливі два випадки: або . Розглянемо функцію і аналогічним способом введемо функцію . Так як функція не зберігає одиницю, . Можливі також два випадки: або . Якщо хоч в одному випадку отримали шукане значення, то пункт завершений. Якщо ж в обидвох випадках отримали константи, то згідно з лемою 3(про немонотонну функцію), підставляючи функцію замість усіх змінних константи і тотожні функції, можна отримати заперечення. Отже, заперечення отримане.

2. Отримання константи 0 та 1. Маємо . Згідно з лемою 2(про несамодвоїсту функцію), підставляючи замість усіх змінних функції заперечення(отримане в попередньому пункті) і тотожну функцію, можна отримати константи