Курсовая работа: Спеціальні класи та функціональна повнота системи функцій алгебри логіки. Теорема Поста

3. Отримання кон’юнкції . Маємо функцію . Згідно з лемою4(про нелінійну функцію), підставляючи у функцію замість усіх змінних константи і заперечення(які були отримані у попередніх пунктах доведення), можна отримати кон’юнкцію або заперечення кон’юнкції. Проте на першому етапі заперечення вже отримано, отже, завжди можна отримати кон’юнкцію

Кон’юнкція отримана.

Отже,

Остання рівність випливає з другого пункту теореми 2. Враховуючи лему 1 достатність доведена.

Розділ 4. Постановка і реалізація задачі

Постановка задачі.

Контрольні приклади виконання програми

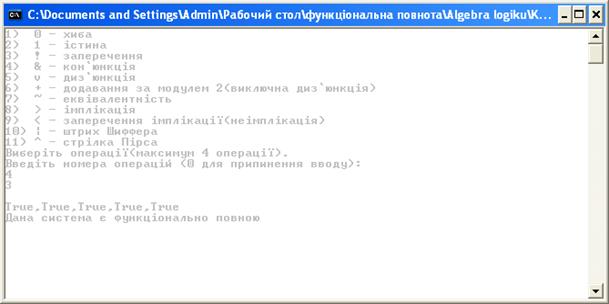
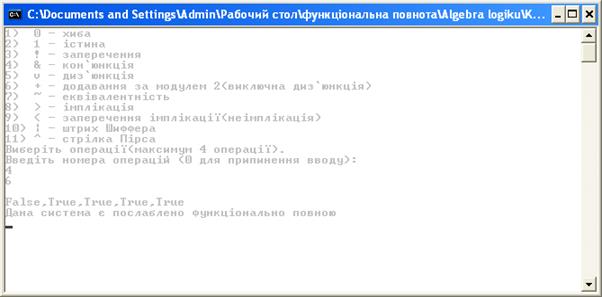
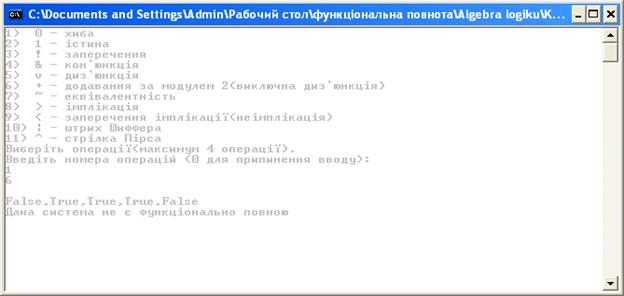
Висновки

Список використаної літератури

1. Алексеев В.Б., Поспелов А.Д. Дискретная математика. – М., 2002. – 44с.

2. Белоусов А.И., Ткачев С.Б. Дискретная математика. –М.,2004. – 743с .

3. Мартинюк О.М. Основи дискретної математики. – Одеса: Наука і техніка, 2008.-300с.

4. Борисенко О.А. Лекції з дискретної математики (множини і логіка): навчальний посібник. – 3-є вид., випр. і доп. – Суми: ВДТ «Університетська книга», 2002. – 180 с.

5. Плотников А.Д. Дискретная математика: учебное пособие. – М.: Новое знание, 2005. – 288 с.

6. Основи дискретної математики Капітонова Ю.В., Кривий С.Л., Летичевський О.А. та ін.– К.: Наукова думка, 2002. – 580 с.