Курсовая работа: Специфика проведения измерений и обработки результатов
8
9
10
11
485
484
483
483
485
Заново определяем значения 
критерия для каждого значения результата серии измерений 
по формуле:
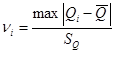
В соответствии с доверительной вероятностью 
с учетом 
находим из соответствующей таблицы значение 
, которое зависит от числа измерений 
и 
.
Условие 
выполняется для всех результатов серии измерений.
Следующим шагом анализа является проверка гипотезы о нормальности распределения оставшихся результатов серии измерений. Проверка выполняется по составному критерию, так как количество результатов серии измерений лежит в диапазоне 10…15<n<40…50.
Применяя первый критерий, следует вычислить отношение:
и сравнить с 
и 
.
Задаемся рекомендуемой доверительной вероятностью 
и для уровня значимости 
определяем из соответствующей таблицы квантили распределения и .
Значение 
соответствует условию 
. Первый критерий выполняется.
Применяя второй критерий, задаемся рекомендуемой доверительной вероятностью 
и для уровня значимости 
с учетом по соответствующим таблицам определяем значения 
и 
.
Для из таблицы для интегральной функции нормированного нормального распределения 
определяем значение 
и рассчитываем E:
, 
.
Используя правила округления, получим:
