Курсовая работа: Специфика проведения измерений и обработки результатов

Задавшись доверительной вероятностью , определяем из соответствующих таблиц интегральной функции нормированного нормального распределения значение и сравниваем с .

Условие выполняется. Различие между средними арифметическими в сериях с доверительной вероятностью можно признать незначимым.

Далее необходимо проверить равнорассеянность результатов измерений в сериях.

Для этого определяем значение:

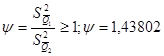
И, задавшись доверительной вероятностью , определяем из соответствующих таблиц значение аргумента интегральной функции распределения вероятности Фишера .

Условие выполняется. Серии с доверительной вероятностью считаем рассеянными.

Выше было показано, что серии равнорассеяны и с незначимым различием средних арифметических. Исходя из этого все результаты измерений объединяются в единый массив и затем для него выполняется обработка по алгоритму, согласно которому необходимо определить оценку результата измерения и среднеквадратического отклонения .

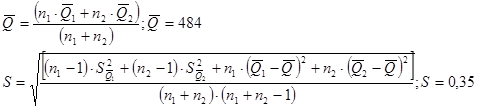
Задавшись доверительной вероятностью , определяем из таблиц распределения Стьюдента значение для числа степеней свободы

Затем определяем доверительный интервал :

Используя правила округления, получим:

Результат измерений запишется в виде:

.

Задание 4. Функциональные преобразования результатов измерений (косвенные измерения)

Условие задания

При многократных измерениях независимых величин и получено по 12 (n) результатов измерений. Эти результаты после внесения поправок представлены в таблице 2. Определить результат вычисления , (вид функции и характер величин представлены в таблице 3).

Вид функциональной зависимости .

Характер и единицы величин:

- ЭДС, мВ;

- сопротивление, Ом;

- сила тока, А.

Обработка результатов измерений величин и проведена в задании 3 первой расчетно-графической работы.