Курсовая работа: Сравнительный анализ методик преобразований Галилея в курсе общей физики и в курсе элементарной физики
В ходе раскрытия этих положений необходимо широко использовать демонстрации (на относительность движения и покоя, траектории и т. д.), киноматериалы (кинокольцовку «Относительность механического движения», видеофильм «Системы отсчета») и рассмотреть задания типа: 1) определить координаты материальной точки в различных системах отсчета; 2) определить основные кинематические характеристики в различных системах отсчета.
Покажем на примере, как следует оформлять решение задачи в этом случае.
Задача. Мимо пункта В одновременно проезжают мотоциклист и велосипедист со скоростями относительно Земли, соответственно равными 20 и 5 м/с. Рассчитайте скорости пункта В , велосипедиста и мотоциклиста в системах отсчета, связанных с Землей (СО «Земля»), с мотоциклистом (СО «мотоциклист»), велосипедистом (СО «велосипедист»), используя классический закон сложения скоростей. Результаты решения занесите в таблицу (табл. 1).
| Объект | Проекция скорости на ось ОХ' , м/с | ||
| в СО «Земля» | в СО «мотоциклист» | в СО «велосипедист» | |
| Пункт В | 0 | -20 | -5 |
| Велосипедист | 5 | -15 | 0 |
| Мотоциклист | 20 | 0 | 15 |
Покажем, как были получены эти результаты, проведя решение задачи.
Решение. Для решения задачи используем классический закон преобразования (сложения) скоростей: скорость тела в неподвижной системе отсчета равна сумме скорости тела в подвижной системе отсчета и скорости самой подвижной системы отсчета: ![]() . Движение происходит вдоль оси ОХ и соответственно закон преобразования (сложения) скоростей записывается через проекции скоростей на ось ОХ :
. Движение происходит вдоль оси ОХ и соответственно закон преобразования (сложения) скоростей записывается через проекции скоростей на ось ОХ : ![]() .
.
1. В системе отсчета, связанной с Землей, скорости заданы в условии задачи и их проекции на ось ОХ соответственно равны: ![]() ;
; ![]() м/с;
м/с; ![]() м/с.
м/с.
2. В системе отсчета, связанной с мотоциклистом:
![]() ;
; ![]() м/с = – 20 м/с;
м/с = – 20 м/с;
![]() ;
; ![]() м/с – 20 м/с = – 15 м/с;
м/с – 20 м/с = – 15 м/с;
![]() ;
; ![]() м/с – 20 м/с = 0.
м/с – 20 м/с = 0.
3. В системе отсчета, связанной с велосипедистом:
![]() ;
; ![]() - 5 м/с = – 5 м/с;
- 5 м/с = – 5 м/с;
![]() ;
; ![]() м/с – 5 м/с = 15 м/с.
м/с – 5 м/с = 15 м/с.
Сведения в таблицу полученных результатов дает наглядное представление об относительности скорости, о роли системы отсчета в определении последней.
Целесообразно показать, что все системы отсчета в кинематике равноправны, но следует выбирать такую систему отсчета, которая приводит к рациональному решению задачи. Для этого целесообразно решить одну и ту же задачу в разных системах отсчета.
Задача. Тело брошено вертикально вверх со скоростью ![]() . Когда тело достигает верхней точки траектории, из того же места и с той же скоростью
. Когда тело достигает верхней точки траектории, из того же места и с той же скоростью ![]() вертикально вверх брошено второе тело. Через сколько времени от момента бросания второго тела произойдет встреча этих тел?
вертикально вверх брошено второе тело. Через сколько времени от момента бросания второго тела произойдет встреча этих тел?
Задачу решают в системе отсчета, связанной с Землей, и в системе отсчета, связанной с одним из тел.
Решение 1. За начало отсчета координаты принимают место бросания тел на Земле. Ось OY направляют вертикально вверх. За начало отсчета времени принимают момент бросания первого тела (рис. 1).
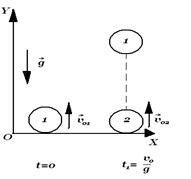
Рис. 1
Записывают уравнение движения для первого тела:
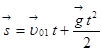 ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Уравнение координаты для первого тела:
![]() ,
,
где ![]() – координата первого тела в любой, произвольный момент времени.
– координата первого тела в любой, произвольный момент времени.
Записывают уравнение движения для второго тела:
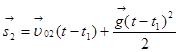 ;
; ![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Уравнение координаты для второго тела: