Курсовая работа: Статистический анализ и прогнозирование
в.) система уравнений имеет однозначное решение относительно совместных зависимых переменных.
Модель должна быть полной, когда необходимо количественно описать экономическое явление или когда она применяется для прогнозирования. Структурная форма важна при конструировании модели, при получении прогнозных значений и принятии решений главная роль принадлежит приведенной, или прогнозной форме.
3. Прогнозная, или приведенная форма эконометрической модели. В данном случае решается система линейных уравнений относительно эндогенных совместно зависимых переменных. Эти переменные являются линейными функциями от предопределенных и возмущающих переменных.
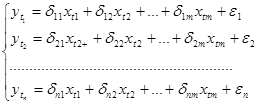
Коэффициенты уравнений в модели являются комбинациями всех структурных коэффициентов совместно зависимых переменных и соответствующих предопределенных переменных во всех структурных уравнениях.
4. Рекурсивная модель. Модель может быть представлена в следующем виде:
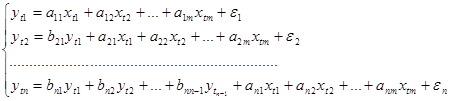
В данной системе линейных уравнений зависимая переменная одного уравнения является фактором в других уравнениях.
5. Модель из системы независимых уравнений. В системе каждая эндогенная переменная ![]() рассматривается как функция одного и того же набора факторов
рассматривается как функция одного и того же набора факторов ![]() .
.
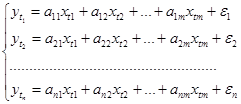
Эндогенные переменные независимы между собой, структурная и приведенная формы таких моделей совпадают.
Проблемы идентификации в эконометрических моделях
При изучении систем одновременных уравнений, описывающих взаимосвязи, каждое структурное уравнение должно быть проверено на идентифицируемость. Идентифицируемость структурных уравнений означает, что посредством линейной комбинации некоторых или всех уравнений модели невозможно получить ни одно уравнение, которое противоречило бы модели и параметры которого отличались бы от параметров структурных уравнений, подлежащих оценке.
Применяются следующие критерии идентифицируемости для полной эконометрической модели.
1. Необходимым, но не достаточным условием идентифицируемости модели является следующее требование-критерий: число предопределенных переменных (D), которые содержатся в модели, но исключены из рассматриваемого структурного уравнения, по крайней мере должно быть равно числу совместно зависимых (эндогенных) переменных (H) в этом же структурном уравнении минус единица.
Критерий можно записать так:
D ≥ H – 1.
При D = H – 1 имеет место точная идентификация, т.е. число ограничений на параметры модели достаточно, чтобы однозначно определять параметры структурных уравнений по их приведенной форме.
При D > H – 1 уравнение сверхидентифицируемо. В данном случае имеется больше ограничений на параметры модели, чем это необходимо для идентификации.
При D < H – 1 структурное уравнение неидентифицируемо, т.к. число ограничений является недостаточным.
2. Необходимое и достаточное условие идентифицируемости модели определяется на основе матрицы. Составленной из коэффициентов при переменных, исключенных из исследуемого уравнения. Ранг этой матрицы должен быть не менее числа совместно зависимых эндогенных переменных минус единица.
Идентификация структурных моделей предполагает, что возмущения распределены независимо друг от друга. Т.к. независимость возмущений является одним из требований рекурсивной модели, рекурсивные модели всегда идентифицируемы.
Оценивание параметров эконометрических моделей
Обыкновенный метод наименьших квадратов может применяться для оценивания параметров системы независимых уравнений, рекурсивных и моделей из взаимозависимых переменных.
Для решения идентифицируемых уравнений применяется косвенный метод наименьших квадратов. Обычный МНК не учитывает одновременных соотношений между совместно зависимыми переменными, поэтому не может непосредственно применяться.
Модель вначале представляется в прогнозной (приведенной) форме. Применяя МНК к каждому полученному уравнению, оценивают все параметры (коэффициенты) системы в прогнозной форме. Так как по предположению все структурные уравнения точно идентифицируемы, на следующем этапе однозначно определяются структурные коэффициенты по коэффициентам прогнозных уравнений. То есть структурные коэффициенты оцениваются косвенно через оценки параметров прогнозной модели.
Для решения сверхидентифицированных уравнений применяется двухшаговый метод наименьших квадратов, учитывающий многосторонние связи совместно зависимых переменных. В данном случае структурные уравнения содержат меньше коэффици