Курсовая работа: Статистическое исследование свойств псевдослучайных чисел получаемых методом Джона фон Неймана

Определить число степеней свободы k.

В приложении 4 по полученным значениям χ2 и k найти вероятность β того, что случайная величина, имеющая χ2-распределение, примет какое-нибудь значение, не меньшее χ20 : P(χ2 χ20) = .

Сформулировать вывод, руководствуясь общим принципом применения критериев согласия, а именно: если вероятность β больше 0.01, то имеющиеся расхождения между теоретическими и опытными частотами следует считать несущественными, а опытное распределение – согласующимся с теоретическим. В противном случае (β<0.01) указанные расхождения признаются неслучайными, а закон распределения, избранный в качестве предполагаемого теоретического, отвергается.

Критерий Колмогорова

На практике кроме критерия χ2 часто используется критерий Колмогорова, в котором в качестве меры расхождения между теоретическими и эмпирическими распределениями рассматривают максимальное значение абсолютной величины разности между эмпирической функцией распределения и соответствующей теоретической функцией распределения

называемое статистикой критерия Колмогорова.

Доказано, что какова бы ни была функция распределения F(x) непрерывной случайной величины X, при неограниченном увеличении числа наблюдений (n) вероятность неравенства P(D) стремится к пределу

задавая уровень значимости α, из соотношения

можно найти соответствующее критическое значение .

Проверка гипотезы о равномерном распределении

При использовании критерия Пирсона для проверки гипотезы о равномерном распределении генеральной совокупности с предполагаемой плотностью вероятности f(x) необходимо вычислив по имеющейся выборке значение, оценить параметры a и b по формулам

,

Где a* и b* - оценки a и b. Действительно, для равномерного распределения

M(X) =

σ== ,

откуда можно получить систему для определения a* и b*:

f(x)=,

решением которой являются выражения (*). Затем, предполагая, что

f(x)=,

можно найти теоретические частоты по формулам:

,

, ,

,

Здесь s – число интервалов, на которые разбита выборка. Наблюдаемое значение критерия Пирсона вычисляется по формуле:

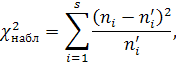
а критическое по таблице с учетом того, что число степеней свободы k=s-3.