Курсовая работа: Статистическое изучение страхового рынка 2
3. Рассчитайте характеристики интервального ряда распределения: среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации, моду и медиану.
4. Вычислить среднюю арифметическую по исходным данным (табл. 2.1), сравнить её с аналогичным показателем, рассчитанным в п. 3 для интервального ряда распределения. Объяснить причину их расхождения.
Сделайте выводы по результатам выполнения задания.
Выполнение задания №1
Целью выполнения данного задания является изучение состава и структуры выборочной совокупности организаций путем построения и анализа статистического ряда распределения организаций по признаку доходов.
1.Построение интервального ряда распределения организаций по доходам
Для построения интервального вариационного ряда, характеризующего распределение организаций по доходам, необходимо вычислить величину и границы интервалов ряда .
При построении ряда с равными интервалами величина интервала h определяется по формуле
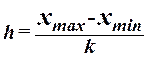 , (1)
, (1)
где ![]() – наибольшее и наименьшее значения признака в исследуемой совокупности, k - число групп интервального ряда.
– наибольшее и наименьшее значения признака в исследуемой совокупности, k - число групп интервального ряда.
Определение величины интервала по формуле (1) при заданных k = 5, xmax = 16,0 млн. руб., xmin = 6,0 млн. руб.:
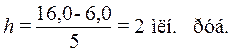
При h = 2 млн. руб. границы интервалов ряда распределения имеют следующий вид (табл.2.2):
Таблица 2.2.
| Номер группы | Нижняя граница, млн. руб. | Верхняя граница, млн. руб. |
| I | 6,0 | 8,0 |
| II | 8,0 | 10,0 |
| III | 10,0 | 12,0 |
| IV | 12,0 | 14,0 |
| V | 14,0 | 16,0 |
Для построения интервального ряда необходимо подсчитать число организаций, входящих в каждую группу (частоты групп ). При этом возникает вопрос, в какую группу включать единицы совокупности, у которых значения признака выступают одновременно и верхней, и нижней границами смежных интервалов (для демонстрационного примера – это 8,0, 10,0, 12,0, 14,0 млн. руб.). Отнесение таких единиц к одной из двух смежных групп рекомендуется осуществлять по принципу полуоткрытого интервала [ ). Т.к. при этом верхние границы интервалов не принадлежат данным интервалам, то соответствующие им единицы совокупности включаются не в данную группу, а в следующую. В последний интервал включаются и нижняя , и верхняя границы .
Процесс группировки единиц совокупности по признаку Доходам представлен во вспомогательной (разработочной) таблице 2.3.
Таблица 2.3.
Группировка страховых организаций по размеру денежных доходов
| Группы | Группы страховых организаций по доходам, млн. руб. | Номер организации | Доходы, млн. руб. | Прибыль млн. руб. |
| 7 | 6,0 | 0,25 | ||
| I | 6,0-8,0 | 15 | 7,0 | 0,31 |
| 16 | 8,0 | 0,40 | ||
| Итого | 3 | 21 | 0,96 | |
| 1 | 9,7 | 0,41 | ||
| 2 | 9,0 | 0,40 | ||
| 5 | 9,8 | 0,42 | ||
| II | 8,0-10,0 | 6 | 10,0 | 0,44 |
| 14 | 8,5 | 0,38 | ||
| 23 | 8,5 | 0,34 | ||
| 24 | 8,5 | 0,35 | ||
| Итого | 7 | 64 | 2,74 | |
| 3 | 10,2 | 0,45 | ||
| 4 | 10,3 | 0,46 | ||
| 8 | 10,5 | 0,48 | ||
| 10 | 11,6 | 0,53 | ||
| III | 10,0-12,0 | 11 | 11,7 | 0,54 |
| 13 | 11,9 | 0,55 | ||
| 20 | 10,5 | 0,49 | ||
| 21 | 10,7 | 0,50 | ||
| 22 | 10,8 | 0,50 | ||
| 26 | 11,5 | 0,52 | ||
| Итого | 10 | 109,7 | 5,02 | |
| 12 | 12,8 | 0,56 | ||
| 17 | 12,2 | 0,58 | ||
| 18 | 13,5 | 0,63 | ||
| IV | 12,0-14,0 | 19 | 13,9 | 0,65 |
| 25 | 12,2 | 0,58 | ||
| 27 | 13,3 | 0,60 | ||
| 28 | 13,8 | 0,64 | ||
| 30 | 13,5 | 0,64 | ||
| Итого | 8 | 105,2 | 4,88 | |
| V | 14,0-16,0 | 9 | 16,0 | 0,75 |
| 29 | 15,0 | 0,70 | ||
| Итого | 2 | 31,0 | 1,45 | |
| Итого | 30 | 330,9 | 15,05 |
В результате группировке получили следующий ряд распределения (таблица 2.4.):
Таблица 2.4.
Распределение страховых организаций по доходам
| Группы | Группы организаций по доходам страховых организаций, млн. руб. | Число организаций |
| I | 6,0-8,0 | 3 |
| II | 8,0-10,0 | 7 |
| III | 10,0-12,0 | 10 |
| IV | 12,0-14,0 | 8 |
| V | 14,0-16,0 | 2 |
Помимо частот групп в абсолютном выражении в анализе интервальных рядов используются ещё три характеристики ряда, приведенные в графах 4 - 6 табл. 1.4. Это частоты групп в относительном выражении, накопленные (кумулятивные) частотыSj ,получаемые путем последовательного суммирования частот всех предшествующих (j-1) интервалов, и накопленные частости, рассчитываемые по формуле 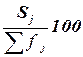 .
.
Таблица 2.5. Структура организаций по доходам
| № группы | Группы организаций по доходам, млн. руб. | Число организаций, fj | Накопленная частота, Sj | Накопленная частость, % | |
| в абсолютном выражении | в % к итогу | ||||
| 1 | 2 | 3 | 4 | 5 | 6 |
| I | 6,0-8,0 | 3 | 10,0 | 3 | 10,0 |
| II | 8,0-10,0 | 7 | 23,33 | 10 | 33,33 |
| III | 10,0-12,0 | 10 | 33,33 | 20 | 66,66 |
| IV | 12,0-14,0 | 8 | 26,67 | 28 | 93,33 |
| V | 14,0-16,0 | 2 | 6,67 | 30 | 100,0 |
| Итого | 30 | 100,0 | |||
Вывод. Анализ интервального ряда распределения изучаемой совокупности страховых организаций показывает, что распределение организаций по доходам не является равномерным: преобладают организации с доходами от 10 млн. руб. до 12 млн. руб. (это 10 организаций, доля которых составляет 33,33 %); 33,33 % организаций имеют доходы менее 10 млн. руб., а 66,66 % – менее 12 млн. руб.
1.2. Нахождение моды и медианы полученного интервального ряда распределения графическим методом
Мода и медиана являются структурными средними величинами , характеризующими (наряду со средней арифметической) центр распределения единиц совокупности по изучаемому признаку.
Мода Мо для дискретного ряда – это значение признака, наиболее часто встречающееся у единиц исследуемой совокупности. В интервальном вариационном ряду модой приближенно считается центральное значение модального интервала (имеющего наибольшую частоту). Более точно моду можно определить графическим методом по гистограмме ряда (рис.1).
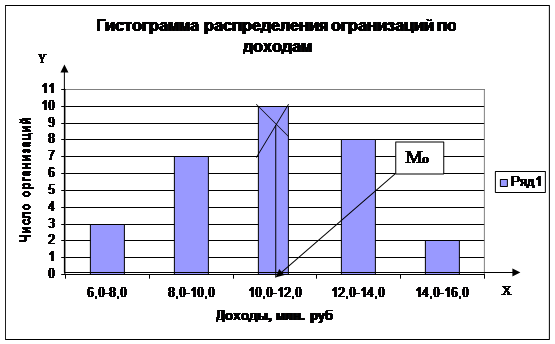
Рис. 1 Определение моды графическим методом
Медиана Ме – это значение признака, приходящееся на середину ранжированного ряда. По обе стороны от медианы находится одинаковое количество единиц совокупности.
Медиану можно определить графическим методом по кумулятивной кривой (рис. 2). Кумулята строится по накопленным частотам (табл. 2.5, графа 5).
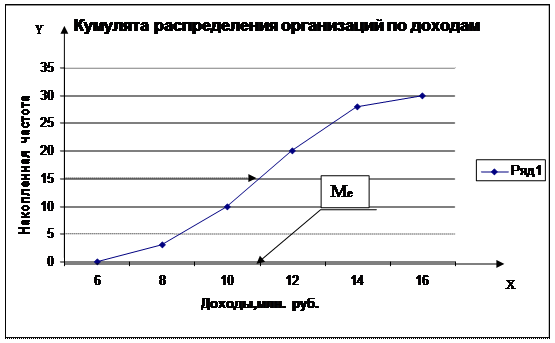
Рис. 2. Определение медианы графическим методом
3. Расчет характеристик ряда распределения
Для расчета характеристик ряда распределения среднюю арифметическую, среднее квадратическое отклонение, коэффициент вариации, моду и медиану на основе табл. 2.5 строится вспомогательная таблица.