Курсовая работа: Статистичні індекси та їх значення в економічних дослідженнях

індекс ціни змінного складу

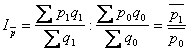(1.21)

Індекс постійного складу показує зміну (в%) середнього значення показника під впливом одного фактора - динаміки його індивідуальних значень. У цьому індексі індексується (змінюється) якісний показник, а кількісний фіксується на рівні звітного періоду.

індекс ціни постійного складу:

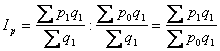(1.22)

Індекс структурних зрушень показує, на скільки процентів змінилося середнє значення показника під впливом змін у структурі сукупності. У даному випадку індексується кількісний показник, а якісний фіксується на рівні базисного періоду.

індекс структурних зрушень ціни:

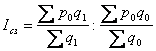(1.23)

Між названими трьома індексами існує взаємозв’язок: індекс змінного складу дорівнює добутку індексу постійного складу та індексу структурних зрушень. Отже,

(1.24)

На основі вказаних індексів можна визначити приріст середнього значення показника в абсолютному виразі загальний та за рахунок окремих факторів - якісного та кількісного (структурного). Наприклад,

приріст середньої ціни (загальний):

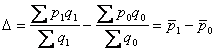(1.25)

приріст середньої ціни за рахунок зміни цін:

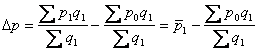(1.26)

приріст середньої ціни за рахунок структурних зрушень:

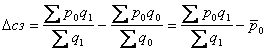(1.27)

1.5 Агрегатні статистичні індекси та факторний аналіз

Основною формою загальних індексів є агрегатні індекси . Своя назва вони одержали від латинського слова „ aggrego", що означає „приєдную” . У чисельнику і знаменнику загальних індексів в агрегатній формі містяться з'єднані набори (агрегати) елементів досліджуваних статистичних сукупностей.

Досягнення в складних статистичних сукупностях порівнянності різнорідних одиниць здійснюється введенням в індексні відносини спеціальних співмножників величин, що індексуються. У літературі такі співмножники називаються співвимірниками . Вони необхідні для переходу від натуральних вимірників різнорідних одиниць статистичної сукупності до однорідних показників. При цьому в чисельнику і знаменнику загального індексу змінюється лише значення величини, що індексується, а їх співвимірниками є постійними величинами і фіксуються на одному рівні (поточного чи базисного періоду). Це необхідно для того, щоб на величині індексу позначався лише вплив фактора, що визначає зміну величини, яка індексується.

У якості співвимірників величин, що індексуються виступають тісно пов'язані з ними економічні показники: ціни, кількості й ін. Добуток кожної величини, що індексується на співвимірник утворить в індексному відношенні визначені економічні категорії.

Агрегатні індекси відносяться до загальних індексів, які характеризують середню зміну індексованого показника у часі та просторі. В агрегатних індексах у чисельнику та знаменнику знаходяться суми добутків двох взаємопов'язаних показників, один з яких - якісний, а другий - кількісний. Позначаються агрегатні індекси літерою І з підстроковим символом індексованого показника.

В залежності від правил побудови агрегатний індексів розрізняють індексні системи Ласпейреса, Пааше та Фішера. В статистиці України використовується комбінована система агрегатних індексів, яка будується за наступними правилами [8].

При визначенні загального індексу цін в агрегатній формі Іp у якості співвимірника величин, що індексуються р ₁ і р ₀ можуть застосовуватися дані про кількість реалізації товарів у поточному періоді q ₁ При множенні q ₁ на величини, які індексуються в чисельнику індексного відношення утвориться значення p ₁ q ₁ , тобто сума вартості продажу товарів у поточному періоді за цінами того ж поточного періоду. У знаменнику індексного відношення утвориться значення p ₀ q ₁ , тобто сума вартості продажу товарів у поточному періоді за цінами базисного періоду. В агрегатних індексах якісних показників індексований показник у чисельнику береться за звітний період, а у знаменнику - за базисний, а співмножник (кількісний показник) у чисельнику і знаменнику фіксується на рівні звітного періоду (метод Пааше). Таким чином, у чисельнику агрегатного індексу якісного показника знаходиться сума значень об'ємного показника за звітний період, а у знаменнику - розрахункові значення об'ємного показника у звітному періоді при умові збереження якісного показника на базисному рівні. Агрегатна формула такого загального індексу має наступний вид:

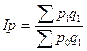(1.28)

Розрахунок агрегатного індексу цін по формулі (1.28) запропонований німецьким економістом Г. Пааше. Тому індекс (1.28) прийнято називати індексом Пааше .

При порівнянні чисельника і знаменника формули (1.28) у різниці визначається показник абсолютного приросту товарообігу за рахунок фактора зміни цін у поточному періоді в порівнянні з базисним періодом:

, (1.29)

В агрегатний індексах кількісних показників індексований індексований показник у чисельнику береться за звітний період, а у знаменнику за базисний, а співмножник (якісний показник) у чисельнику і знаменнику фіксується, тобто береться однаковим, на рівні базисного періоду (метод Ласпейреса). Отже, у знаменнику агрегатних індексів кількісних показників знаходиться сума значень об'ємного показника за базисний період, а у чисельнику - розрахункові значення об'ємного показника при умові збереження якісного показника на базисному рівні.

При цьому способі визначення агрегатного індексу цін у якості співвимірника величин, що індексуються р ₁ і р ₀ можуть застосовуватися дані про кількість реалізації товарів у базисному періоді q ₀ . При цьому множення q ₀ на величини, що індексуються в чисельнику індексного відношення утворить значення p ₁ q ₀ , тобто суму вартості продажу товарів у базисному періоді за цінами поточного періоду. У знаменнику індексного відношення утвориться значення p ₀ q ₀ тобто сума вартості продажу товарів у базисному періоді за цінами того ж базисного періоду. Агрегатна форма такого загального індексу має вид: