Курсовая работа: Статистичні індекси та їх значення в економічних дослідженнях

Розрахунок загального індексу цін за формулою (1.30) запропонований німецьким економістом Е. Ласпейресом. Тому індекс цін, розрахований по цій формулі, прийнято називати індексом Ласпейреса .

При порівнянні чисельника і знаменника формули (1.30) визначається показник приросту товарообігу при продажі товарів у базисному періоді за цінами поточного періоду:

∑∆qp (p) = ∑p ₁ q ₁ - ∑p ₀ q ₀ , (1.31)

Таким чином, виконані по формулах (1.28) і (1.30) розрахунки мають різні показання індексів цін. Це порозумівається тим, що індекси Пааше і Ласпейреса характеризують різні якісні особливості зміни цін.

Індекс Пааше характеризує вплив зміни цін на вартість товарів, реалізованих у звітному періоді. Індекс Ласпейреса показує вплив зміни цін на вартість кількості товарів, реалізованих у базисному періоді.

Застосування індексів Пааше і Ласпейреса залежить від мети дослідження. Якщо аналіз проводиться для визначення економічного ефекту від зміни цін у звітному періоді в порівнянні з базисним, то застосовується індекс Пааше, що відображає різницю між фактичною вартістю продажу товарів у звітному періоді (∑p ₁ q ₁ ) і розрахунковою вартістю продажу цих же товарів за базисними цінами (∑р ₀ q ₁ ).

Якщо метою аналізу є визначення обсягу товарообігу при продажі в майбутньому періоді такої ж кількості товарів, що й у базисному періоді, але за новими цінами, то застосовується індекс Ласпейреса. Цей індекс дозволяє обчислювати різниця між сумою фактичного товарообігу базисного періоду (∑p ₀ q ₀ ) і можливого обсягу товарообігу при продажу тих же товарів за новими цінами (∑p ₁ q ₀ ). Ці особливості індексу Ласпейреса обумовлюють його застосування при прогнозуванні обсягу товарообігу в зв'язку з намічуваними змінами цін на товари в майбутньому періоді.

Разом з тим, при вивченні звітних даних, коли метою аналізу є кількісна оцінка зміни обсягу товарообігу в результаті зміни цін, що відбулася, у звітному періоді, для визначення загального індексу цін і одержуваного при цьому економічного ефекту застосовується формула Пааше.

В агрегатних індексах об'ємних показників у чисельнику знаходиться сума добутків якісного і кількісного показників за звітний період, а у знаменнику - за базисний, тобто індексуються обидва показники (метод Фішера).

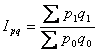(1.32)

Отже, в чисельнику цих індексів сумуються значення об'ємного показника за звітний період, а у знаменнику - за базисний.

Між агрегатними індексами показників існує взаємозв'язок: агрегатний індекс об'ємного показника дорівнює добутку агрегатних індексів якісного та кількісного показників.

Зв’язок соціально-економічних явищ і процесів знаходить своє відображення у взаємозв’язку показників: ряд економічних показників можна подати як добуток кількох інших. Це мультиплікативна форма зв’язку. Співмножники виступають як факторні показники, від величини яких функціонально залежить результат: У зв’язку з цим при аналізі динаміки соціально-економічних явищ виникає потреба визначити роль окремих факторів у зміні результативного показника, що має досить істотне практичне значення. Індексний метод дозволяє оцінити вплив окремих факторів. Оцінка може бути здійснена як у відносному, так і в абсолютному вираженні. Оцінити вплив кожного з факторів означає обчислити індекси факторних показників відповідної системи спів залежних індексів. У загальному вигляді всі двофакторні зведені індекси поєднані так:

або 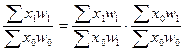(1.33)

Визначення абсолютного приросту результативного показника за рахунок зміни кожного фактора теж здійснюється при побудові системи індексів. Якщо йдеться про окремий вид явища, то використовують систему індивідуальних індексів. При цьому слід будувати індекси з урахуванням специфіки індексного методу, яка полягає у зважуванні і фіксуванні ваги. Абсолютні прирости за рахунок окремих факторів обчислюють як різницю між чисельником і знаменником відповідних факторних індексів. Так, загальний абсолютний приріст

(1.34)

Його можна розкласти за факторами

(1.35)

При такому методі розкладання абсолютного приросту за факторами буде дорівнювати . Цей метод називають ланцюгових підстановок. Відносно індивідуальних індексів за умови, що результативний показник, поданий як добуток двох факторів - співмножників, можна зробити такий висновок: абсолютний приріст результативного показника за рахунок екстенсивного фактора w дорівнює приросту цього фактора, помноженому на базисний рівень інтенсивного фактора x ₀ ; приріст за рахунок інтенсивного фактора x до