Курсовая работа: Статистистический анализ туризма и отдыха в Краснодарском крае

В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин.

В зависимости от того, как выражают уровни ряда состояние явления на определенные моменты времени (на начало месяца, квартала, года и т. п.) или его величину за определенные интервалы времени (например, за сутки, месяц, год и т. п.), различают соответственно моментные и интервальные ряды динамики.

Уровни этого ряда - обобщающие итоги статистики вкладов населения по состоянию на определенную дату (на начало каждого месяца).

Из различного характера интервальных и моментных рядов динамики вытекают некоторые особенности уровней соответствующих рядов.

Уровни интервального ряда динамики абсолютных величин характеризуют собой суммарный итог какого-либо явления за определенный отрезок времени. Они зависят от продолжительности этого периода времени, и поэтому их можно суммировать как не содержащие повторного счета.

Отдельные же уровни моментного ряда динамики абсолютных величин содержат элементы повторного счета, например, число вкладов населения, учитываемых за январь, существует и в настоящее время, являясь единицами совокупности и в июне. Все это делает бессмысленным суммирование уровней моментных рядов динамики.

В зависимости от расстояния между уровнями ряды динамики подразделяются на ряды динамики с равноотстоящими уровнями и не равноотстоящими уровнями во времени.

Ряды динамики следующих друг за другом периодов или следующих через определенные промежутки дат называются равноотстоящими (см. пример о числе вкладов в Сбербанк РФ за январь - июнь 1997 г.). Если же в рядах даются прерывающиеся периоды или неравномерные промежутки между датами, то ряды называются не равноотстоящими.

В зависимости от наличия основной тенденции изучаемого процесса ряды динамики подразделяются на стационарные и не стационарные.

Если математическое ожидание значения признака и дисперсия (основные характеристики случайного процесса) постоянны, не зависят от времени, то процесс считается стационарным и ряды динамики также называются стационарными. Экономические процессы во времени обычно не являются стационарными, так как содержат основную тенденцию развития, но их можно преобразовать в стационарные путем исключения тенденций.

Все явления и процессы, характеризующие социально-экономическое развитие и составляющие единую систему национальных счетов, тесно взаимосвязаны и взаимозависимы между собой. В статистике показатели; характеризующие эти явления, могут быть связаны либо корреляционной зависимостью, либо быть независимыми. Корреляционная зависимость является частным случаем стохастической зависимости, при которой изменение значений факторных признаков (x1, x2, …,xk) влечет за собой изменение среднего значения результативного признака. Корреляционная зависимость исследуется с помощью методов корреляционного и регрессионного анализов.

Корреляционный анализ изучает взаимосвязи показателей и позволяет решить следующие задачи:

Оценка тесноты связи между показателями с помощью парных, частных и множественных коэффициентов корреляции

Оценка уравнения регрессии.

Основной предпосылкой применения корреляционного анализа является необходимость подчинения совокупности значений всех факторных (x1, x2, …,xk) и результативного (У) признаков k-мерному нормальному закону распределения или близость к нему. Если объем исследуемой совокупности достаточно большой (n > 50), то нормальность распределения может быть подтверждена на основе расчета и анализа критериев Пирсона, Ястремского, Боярского, Колмогорова, чисел Вастергарда и т. д. Если n <. 50, то закон распределения исходных данных определяется на базе построения и визуального анализа поля корреляции. При этом если в расположении точек имеет место линейная тенденция, то можно предположить, что совокупность исходных данных (У, x1, x2, …,xk) подчиняется нормальному распределению.

Целью регрессионного анализа является оценка функциональной зависимости условного среднего значения результативного признака (У) от факторных (x1, x2, …,xk). Основной предпосылкой регрессионного анализа является то, что только результативный признак (У) подчиняется нормальному закону распределения, а факторные признаки x1, x2, …,xk могут иметь произвольный закон распределения. В анализе динамических рядов в качестве факторного признака выступает время t. При этом в регрессионном анализе заранее подразумевается наличие причинно-следственных связей между результативным (У) и факторными (x1, x2, …,xk) признаками. Уравнение регрессии, или статистическая модель связи социально-экономических явлений, выражаемая функцией

Линейный коэффициент корреляции

Линейный коэффициент корреляции был впервые введен вначале 90-х гг. Пирсоном, Эджвортом и Велдоном и характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости. В теории разработаны и на практике применяются различные модификации формул расчета данного коэффициента.

Мы будем проводить расчет по итоговым значениям исходных переменных, линейный коэффициент корреляции, который можно вычислить по формуле:

, (1)

или

(2)

Линейный коэффициент корреляции имеет большое значение при исследовании социально-экономических явлений и процессов, распределение которых близко к нормальному. Легко доказывается, что условие r = 0 является необходимым и достаточным для того, чтобы величины Х и У были независимы. При этом условии коэффициенты регрессии ayx, axy также обращаются в нуль, а прямые регрессии У по Х и Х по У оказываются взаимно перпендикулярными (параллельными: одна оси абсцисс, а вторая оси ординат).

Если же r = 1, то это означает, что все точки (Х, У) находятся на прямой и зависимость между Х и У является функциональной. Прямые регрессии в этом случае совпадают. Указанное положение распространяется также на случай нормального распределения трех и более величин.

Линейный коэффициент корреляции изменяется в пределах от - 1 до 1: - 1 r 1. Знаки коэффициентов регрессии и корреляции совпадают. При этом интерпретацию выходных значений.

Зависимость хозяйственных результатов туризма от спроса особенно велика потому, что в структуре эксплуатационных затрат ведущее место принадлежит постоянной части, а не переменной:

постоянные затраты, то есть зависимость от объема загрузки отеля, которые возникают сразу же после гостиницы, с первых шагов её эксплуатации. Отель несет постоянные затраты, даже если в нем нет ни одного клиента. Они состоят из амортизации основных фондов, большей части зарплаты, значительных эксплуатационных затрат. Величина последних затрат при нормальном режиме работы составляет 50-70% их общего объема;

переменные затраты, то есть такие, которые, как правило, пропорционально возрастают по мере увеличения потребления услуг гостиницы. Они включают заметную часть расходов на содержание и ремонт отеля, расходов на заработную плату и т.д.

Поскольку в эксплуатационных затратах значительная доля принадлежит постоянным расходам, то с увеличением загрузки отеля резко снижает себестоимость ночевки. По эмпирическим расчетам получается, что рост вместимости на 10% ведет к снижению себестоимости на 6-7%.

Показателем, характеризующим использование гостиничных ресурсов, является коэффициент использования вместимости, или коэффициент загрузки Кв.

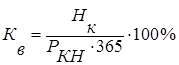, (3)