Также в этом модуле программы реализованы вспомогательные функции такие как:

- Вычисление функции вероятности нормального распределения со средним 0 и ско 1.

- Вычисление обратной функции вероятности нормального распределения.

- Вычисление определителя матрицы.

- Решение системы с помощью LU-разложения.

Благодаря третьему модулю, который отвечает за визуализацию, пользователь имеет возможность, получать некоторые промежуточные результаты, в зависимости от них вводить различные параметры и корректировать работу программы.

Весь алгоритм программы можно представить в виде блок-схемы (рис.1).

Рис. 1. Блок-схема алгоритма.

3. ОПИСАНИЕ РЕЗУЛЬТАТОВ

3.1 Исходные данные

Исходные данные (рис. 2) для разработки стохастической модели были предоставлены ГУ "ГГО" по станции, расположенной на ул. Пестеля (г. Санкт-Петербург). Эти данные характеризуют загрязнение атмосферного воздуха озоном за 2002 год.

В разрабатываемой стохастической модели связь межу предиктантом и предикторами описывается в виде , где

- - предиктант, максимальная за сутки концентрация озона (мкг/м3);

- – линейная функция от n предикторов;

- в качестве предикторов используются следующие величины:

- максимальная концентрация озона (мкг/м3) за предыдущие сутки;

-7- концентрация оксида азота (мкг/м), измеренная в 7 часов;

-7 - концентрация диоксида азота (мкг/м3), измеренная в 7 часов;

- концентрация озона (мкг/м3), измеренная в 7 часов;

- скорость ветра (м/с) в 6 и 12 часов;

- направление ветра (дес.град) в 6 и 12 часов;

- атмосферное давление (мб) в 6 и 12 часов;

- температура воздуха (°С) в 6 и 12 часов;

- относительная влажность воздуха (%) в 6 и 12 часов;

- атмосферные явления (шифр), наблюдаемые в 6 и 12 часов.

Длина массива данных составляет 273.

Рис.2. Исходные данные

3.2 Подготовительный этап

Чтобы вычислить коэффициенты функции при каждом из предикторов необходимо подготовить исходные данные. С этой целью:

1. Ряд значений максимальных за сутки концентраций озона разбивается на обучающую и независимую выборки. Далее все преобразования производятся только с обучающей выборкой.

2. Осуществляется цензурирование выборки: сортируется массив данных в соответствие с ростом переменной , где - значение за сутки до срока, на который дается прогноз. Находим значение 60%-ного квантиля функции распределения . - В рассматриваемом примере значению 60%-ного квантиля функции распределения соответствует концентрация = 63,42 мкг/м3. Делим исходные данные на две группы. В первую группу, объем которой составляет 60% от общей выборки, войдут значения , сопутствующие метеоусловия и расчетные параметры, которые наблюдались при < 63,42 мкг/м3. Для этой группы прогноз осуществляется по уравнению . Во вторую группу, объем которой составляет 40% от общей выборки, - значения , , , , сопутствующие метеоусловия и расчетные параметры, которые наблюдались при >= 63,42 мкг/м3. Для этой группы прогноз осуществляется с использованием прогностических схем.

3.3 Преобразование предикторов

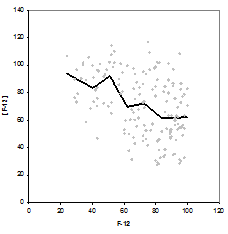
1. Линеаризация (рис.3). Исключение нелинейности связей между предиктантом и предикторами.