Курсовая работа: Строение идеалов полукольца натуральных чисел

Доказательство. Рассмотрим. По теоремам 2 и 5 . Значит, начиная с элемента все элементы вида где Заметим, что Из условия следует, что тогда ‒ полная система вычетов по модулю a, обозначим ее (*).

Рассмотрим число

Числа можем получить из системы вычетов (*), прибавляя к ним значит, все они лежат в идеале I. Число так как а Таким образом, нашли a подряд идущих чисел, принадлежащих идеалу I, и число перед ними, не принадлежащее I. Производя подстановку и преобразовывая выражение получаем искомый элемент с.

Обобщим результат, полученный в теореме 8:

Теорема 9. Пусть , Обозначим

, ,…,

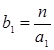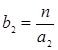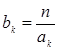
Тогда

.

Доказательство. База метода математической индукции для значений k=2,3 доказана в теоремах 7 и 8. Предположив, что выполняется , доказательство проводится аналогично доказательству теоремы 8.

Предложение. В порожденном идеале выполняется .

Доказательство. Если , то найдется, по крайней мере, пара образующих и , , сравнимых по модулю . Тогда выражается через и , противоречие.

Крайний случай доказанного выше отношения позволяет найти элемент .

Теорема 10. .

Доказательство. Заметим, что образующие образуют полную систему вычетов по модулю . Рассмотрим еще одну полную систему вычетов по тому же вычету . Для произвольного найдется в точности один образующий , сравнимый с по модулю . Тогда для некоторого , откуда следует . Получили, что подряд идущих элементов из лежат в . Поскольку, очевидно,

, то

Теорема 11. Если ‒ наименьший образующий -порожденного идеала , то , причем обе оценки точные.

Доказательство. Пусть ‒ семейство образующих идеала . До полной системы вычетов по модулю не хватает одного числа. Обозначим через наименьшее число из идеала , дополняющее до полной системы. Заметим, что для некоторого . Отсюда легко получаем, что наименьшее возможное значение, которое может принять , равно . Число не лежит в идеале , получаем оценку.

С другой стороны, , а в случае равенства числа лежат в . Действительно, каждое из них сравнимо по модулю с некоторым образующим и , откуда . Это дает оценку . Не сложно проверить, что точность обеих полученных оценок дают соответственно идеалы

и .

В общем случае проблема нахождения элемента с представляется на данный момент неразрешимой. Однако для дальнейшего ее изучения может быть использована специально разработанная программа "FindC", которая позволяет находить элемент с для введенной системы образующих, причем она может быть не упорядоченной по возрастанию и содержать элементы, линейно выражающиеся через другие.

Действия программы:

1. Сортирует введенные образующие в порядке возрастания (процедура Sort).

2. Проверяет систему на наличие элементов, линейно выражающихся через другие, в случае наличия таковых выводит их и линейную комбинацию (осуществляется с помощью процедуры Lin).

3. Выводит линейно независимую систему образующих, находит их НОД (процедура NOD). Если НОД1, то осуществляется деление каждой образующей на НОД, дальнейшая работа происходит с новой системой.

4. Проверяет элементы полукольца , начиная с 2, на возможность выражения их в виде линейной комбинации системы образующих. При нахождении подряд идущих элементов , принадлежащих идеалу, можно сделать вывод о том, что и последующие элементы также принадлежат идеалу, и программа умножает элемент, на меньше текущего, на НОД, и это произведение будет искомым элементом c.

Библиографический список

1. Абрамов А.М. Квант, №3, 1984. с. 40-41.