Курсовая работа: Структурный синтез перестраиваемых arc-схем.
Для снижения влияния электронных ключей на характеристики и параметры устройства целесообразно в качестве базисных структур использовать интеграторы (Si (p)), что в общем случае с переменной постоянной времени (ti ), и усилители (Kj (p)) с управляемым коэффициентом передачи (Kj ). Эти блоки объединяются в структуры посредством коммутирующей части схемы (КЧС), которая также связывает их с источником сигнала x0 и входным узлом схем y0 (рис. 1).
Рассматриваемая модель перестраиваемого устройства описывается следующей матрично-векторной системой уравнений:
 (1)
(1)
Смысл векторов XS , XK , YS , YK , поясняется векторным сигнальным графом, изображенным на рис. 1. Структура матриц BSS , BSK , BKS , BKK и векторов TK , TS , AK , AS , относящихся к КЧС, приведена в табл. 1, где знак Т означает транспонирование.
Из векторного графа следует, что данная модель состоит из трех основных частей. Первая часть (компоненты векторов AK и AS ) является расщепителем, который посредством разветвления преобразует скалярную величину входного сигнала x 0 в векторную, воздействующую на соответствующие входы базисных структур. Вторая и наиболее важная часть системы (компоненты всех матриц, входящих в (2)) осуществляет основную операцию над векторными сигналами XS и XK , преобразуя их в Ys , YK . Здесь сосредоточены физически осуществимые принципы формирования коэффициентов полинома знаменателя передаточной функции и заложены основы конструирования коэффициентов полинома числителя. Третья часть (компоненты векторов TS , TK и скаляр t0 ) реализует сумматор, обеспечивающий связь с выходами базисных структур.

Рис. 1. Обобщенная структура перестраиваемого ARC-устройства

Рис. 2. Векторный сигнальный граф обобщенной структуры
Таблица 1
Компоненты коммутирующей части схемы
| Матрица, вектор | Размерность | Физический смысл компонент (передача КЧС) |
|
|
| от выхода i-го интегратора ко входу l-го интегратора |
|
|
| от выхода i-го интегратора ко входу q-го усилителя |
|
|
| от выхода j-го усилителя ко входу l-го усилителя |
|
|
| от выхода j-го усилителя ко входу l-го интегратора |
|
|
| от выхода i-го интегратора к нагрузке |
|
|
| от выхода j-го усилителя к нагрузке |
|
|
| от генератора ко входу i-го интегратора |
|
|
| от генератора ко входу j-го усилителя |
Для обеспечения пассивности КЧС необходимо выполнить условия
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
гарантирующие возможность ее построения на базе резисторов, причем для любого h-го усилителя с фиксированным коэффициентом передачи возможна реализация отрицательных передач ![]() путем использования неинвертирующего входа операционного усилителя (ОУ). В этом случае в неравенстве (2) учитываются модули соответствующих величин. Базисные структуры описываются диагональными матрицами
путем использования неинвертирующего входа операционного усилителя (ОУ). В этом случае в неравенстве (2) учитываются модули соответствующих величин. Базисные структуры описываются диагональными матрицами
![]() (5)
(5)
компоненты которых являются передаточными функциями реальных интеграторов и усилителей, поэтому
 (6)
(6)
 (7)
(7)
где ![]() – площадь и статический коэффициент усиления ОУ, положенного в основу i-го интегратора (j-го усилителя);
– площадь и статический коэффициент усиления ОУ, положенного в основу i-го интегратора (j-го усилителя); ![]() – коэффициент передачи на холостом ходу i-го (j-го) резисторного управителя.
– коэффициент передачи на холостом ходу i-го (j-го) резисторного управителя.
Передаточная функция обобщенной структуры следует из системы векторно-матричных уравнений (1) и при переходе к блочным (клеточным) матрицам и векторам имеет вид:
 . (8)
. (8)
Для идеальных ОУ ![]() блочная матрица основной части системы может быть представлена следующим образом:
блочная матрица основной части системы может быть представлена следующим образом:
 . (9)
. (9)
При решении конкретных задач качественного характера удобным оказывается представление
 (10)
(10)
при этом векторы ![]() , компоненты которых являются передаточными функциями на выходах интегрирующих и масштабных усилителей, определятся после обращения матрицы Lи по формулам Фробениуса [1] из следующих соотношений:
, компоненты которых являются передаточными функциями на выходах интегрирующих и масштабных усилителей, определятся после обращения матрицы Lи по формулам Фробениуса [1] из следующих соотношений:
![]() (11)
(11)
где ![]() .
.
Воспользовавшись методом В.Н. Фаддеевой [6] для вычисления резольвенты матрицы ![]() , функцию (10) можно привести к дробно-рациональному виду
, функцию (10) можно привести к дробно-рациональному виду
 (12)
(12)
где коэффициенты числителя и знаменателя определяются алгоритмом:
 (13)
(13)
Здесь ![]() – след (сумма диагональных элементов) соответствую-щей матрицы.
– след (сумма диагональных элементов) соответствую-щей матрицы.
Приведенный алгоритм позволяет на последнем шаге q = n осуществить контроль результата, т.к. ![]() . Однако он довольно чувствителен к ошибкам округления, поэтому при численных методах решения задачи необходимо предусмотреть перевод компонент матриц в числа с удвоенной точностью.
. Однако он довольно чувствителен к ошибкам округления, поэтому при численных методах решения задачи необходимо предусмотреть перевод компонент матриц в числа с удвоенной точностью.
2. Динамический диапазон перестраиваемых ARC-схем
Верхняя граница динамического диапазона определяется не только максимальным выходным напряжением ОУ ![]() при заданном коэффициенте нелинейных искажений, но и свойствами схемы. В общем случае на выходах ОУ в рабочем диапазоне частот W напряжения могут превышать выходное напряжение схемы, определяемое входным сигналом и максимальным коэффициентом передачи
при заданном коэффициенте нелинейных искажений, но и свойствами схемы. В общем случае на выходах ОУ в рабочем диапазоне частот W напряжения могут превышать выходное напряжение схемы, определяемое входным сигналом и максимальным коэффициентом передачи ![]() . Поэтому их уровень должен определяться соотношением
. Поэтому их уровень должен определяться соотношением
![]() (14)
(14)
где 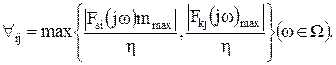
Собственный шум схемы, состоящей из интеграторов и масштабных усилителей, и, следовательно, нижняя граница ее динамического диапазона определяются шумами активных элементов и резисторов. Как правило, шум резисторов можно уменьшить на этапе расчета или параметрической оптимизации схемы соответствующим выбором не только их типов, но и номиналов, поэтому на этапе синтеза можно учитывать только влияние шумов ОУ. В этом случае
![]() (15)
(15)
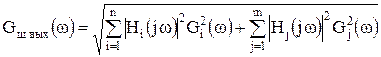 , (16)
, (16)
где ![]() ,
, ![]() – комплексный коэффициент передачи с выхода i-го (j-го) ОУ к нагрузке;
– комплексный коэффициент передачи с выхода i-го (j-го) ОУ к нагрузке; ![]() ,
, ![]() – эквивалентная спектральная плотность мощности источников шумовой модели i-го (j-го) ОУ;
– эквивалентная спектральная плотность мощности источников шумовой модели i-го (j-го) ОУ; ![]() – границы диапазона рабочих частот W.
– границы диапазона рабочих частот W.
Таким образом, мерой динамического диапазона схемы для идентичных ОУ является произведение
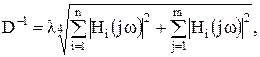 (17)
(17)
которое в процессе синтеза необходимо минимизировать в диапазоне частот W или, если это возможно (например, для узкополосных устройств и звеньев второго порядка), в некоторой особой точке ![]() .
.
Учет влияния параметров активных элементов на обобщенную структуру производится через матрицу
![]() (18)
(18)
вытекающую из системы (1).
Воспользовавшись методом пополнения [87] при обращении этой матрицы, можно установить, что чувствительность
динамический диапазон частотный интеграторный
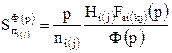 (19)
(19)
определяет влияние i-го (j-го) ОУ на верхний и нижний уровни динамического диапазона схемы, причем ![]() следуют из соотношений (8) при
следуют из соотношений (8) при
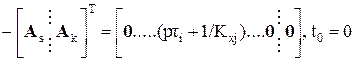 (20)
(20)
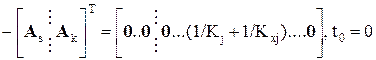 (21)
(21)
--> ЧИТАТЬ ПОЛНОСТЬЮ <--