Курсовая работа: Сущность, модели, границы применения метода производственной функции
где ![]() V* .
V* .
Указанное отображение, вообще говоря, является многозначным, т.е. множество f ( x ) содержит более чем одну точку. Однако для многих реалистичных ситуаций производственные функции оказываются однозначными и даже, как сказано выше, дифференцируемыми. В наиболее простом случае производственная функция есть скалярная функция N аргументов:
![]()
Здесь величина y имеет, как правило, стоимостный характер, выражая объем производимой продукции в денежном выражении. В качестве аргументов выступают объемы затрачиваемых ресурсов при реализации соответствующего эффективного технологического способа. Таким образом, приведенное соотношение описывает границу технологического множества V ,поскольку при данном векторе затрат ( x 1 , ..., x N ) производить продукции, в количестве большем, чем y , невозможно, а производство продукции в количестве меньшем, чем указанное, соответствует неэффективному технологическому способу. Выражение для производственной функции оказывается возможным использовать для оценки эффективности принятого на данном предприятии методе хозяйствования. В самом деле, для заданного набора ресурсов можно определить фактический выпуск продукции и сравнить его с рассчитанным по производственной функции. Полученная разница дает полезный материал для оценки эффективности в абсолютном и относительном измерении.
Производственная функция представляет собой очень полезный аппарат плановых расчетов, и поэтому в настоящее время развит статистический подход к построению производственных функций для конкретных хозяйственных единиц. При этом обычно используется некоторый стандартный набор алгебраических выражений, параметры которых находятся при помощи методов математической статистики. Такой подход означает, в сущности, оценку производственной функции на основе неявного предположения о том, что наблюдаемые производственные процессы являются эффективными. Среди разнообразных типов производственных функций наиболее часто применяются линейные функции вида
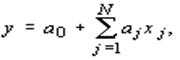
поскольку для них легко решается задача оценивания коэффициентов по статистическим данным, а также степенные функции
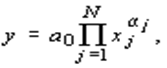
для которых задача нахождения параметров сводится к оцениванию линейной формы путем перехода к логарифмам.
В предположении о дифференцируемости производственной функции в каждой точке множества X возможных комбинаций затрачиваемых ресурсов полезно рассмотреть некоторые связанные с ПФ величины.
В частности, дифференциал
![]()
представляет собой изменение стоимости выпускаемой продукции при переходе от затрат набора ресурсов x = ( x 1 , ..., x N ) к набору x + dx = ( x 1 + dx 1 , ..., x N + dx N ) при условии сохранения свойства эффективности соответствующих технологических способов. Тогда величину частной производной
![]()
можно трактовать как предельную (дифференциальную) ресурсоотдачу или, иными словами, коэффициент предельной продуктивности, который показывает, на сколько увеличится выпуск продукции в связи с увеличением затрат ресурса с номером j на малую единицу. Величина предельной продуктивности ресурса допускает истолкование как верхний предел цены p j , которую производственный объект может уплатить за дополнительную единицу j -того ресурса с тем, чтобы не оказаться в убытках после ее приобретения и использования. В самом деле, ожидаемый прирост продукции в этом случае составит
![]()
и, следовательно, соотношение
![]()
позволит получить дополнительную прибыль.
В коротком периоде, когда один ресурс рассматривается как постоянный, а другой как переменный, большинство производственных функций обладают свойством убывающего предельного продукта. Предельным продуктом переменного ресурса называют прирост общего продукта в связи с увеличением применения данного переменного ресурса на единицу.
Предельный продукт труда можно записать как разность
MPL = F ( K , L + 1) - F ( K , L ),
где MPL предельный продукт труда.
Предельный продукт капитала можно также записать как разность
MPK = F ( K + 1, L ) - F ( K , L ),
где MPK предельный продукт капитала.
Характеристикой производственного объекта является также величина средней ресурсоотдачи (продуктивности производственного фактора)
![]()
имеющего ясный экономический смысл количества выпускаемой продукции в расчете на единицу используемого ресурса (производственного фактора). Величина, обратная к ресурсоотдаче