Курсовая работа: Сжатие данных при телеизмерениях

Рисунок 8

Рассмотрим теперь предсказатель первого порядка. Степень полинома в этом случае m=1. Для построения полинома требуется два предшествующих отсчета, через которые проводится прямая линия. Предсказанное значение для последующих отсчетов лежит на этой линии (рисунок 9).

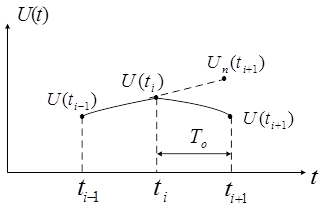
Рисунок 9

Предсказанное для момента времени значение параметра рассчитывается по формуле:

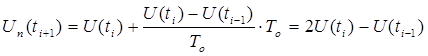. ( 9)

Если ошибка , то отсчет исключается. В этом случае для расчета предсказанного значения в точке используется формула:

. ( 10)

Сжатие с помощью предсказателя первого порядка требует запоминание последнего существенного отсчета и предсказанного значения отсчета (рисунок 10).

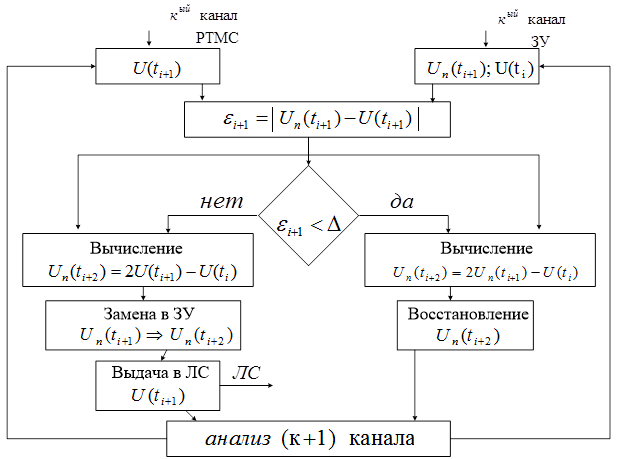
Рисунок 10

Согласно экспериментальным данным при сжатии медленно меняющихся параметров предсказатель нулевого порядка дает коэффициент сжатия около 50, а предсказатель первого порядка – 70. Использование полиномов более высокого порядка даёт небольшое приращение коэффициента сжатие, но приводит к увеличению вычислений и усложнению экстраполятора. Наиболее помехоустойчивы экстраполяторы низких порядков, поэтому обычно используются экстраполяторы нулевого и первого порядка.

3.3 Оптимальное линейное предсказание

Для определения алгоритма оптимального линейного предсказания необходимо знать корреляционную функцию или энергетический спектр параметра. Значения параметра в момент времени предсказывается путем вычисления линейной комбинации предшествующих отсчетов по формуле:

, ( 11)

где коэффициенты выбираются из условия минимальной дисперсии разности предсказанного значения от действительной величины.

. ( 12)

Коэффициенты находятся путем решения системы уравнений вида:

, ( 13)

В случае если используется одно предшествующее значение параметра , то

, , ( 14)

где - коэффициент корреляции параметра, - период опроса.

Если используется два предшествующих значения параметра :

, ( 15)

Алгоритм работы при оптимального линейного предсказания строится также, как и при предсказании нулевого и первого порядка, но вычисление предсказания параметра осуществляется в соответствии с формулами ( 14) и ( 15).

Можно показать, что дисперсия отклонения предсказанного значения от действительного в случае предсказания нулевогопорядка:

, ( 16)

а в случае предсказания первого порядка:

. ( 17)