Курсовая работа: Теорії лінійних одноконтурних автоматичних систем регулювання
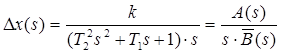
Для переходу від зображення вихідної функції до її оригіналу ∆x (t) можна застосовувати метод О. Хевісайда. Формула Хевісайда:


Якщо корені характеристичного рівняння p2 , p3 - речовинні і уявні, розв’язання:
![]()
2. Побудова кривої розгону об’єкту
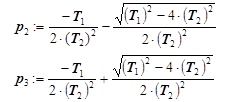
Km: =3.2
τ: =7
T1: =45 T2: =11 m: =0.37 ΔN: =50
P2: = - 0.024 P3: = - 0.348
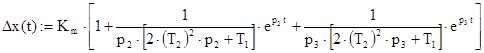
Крива розгону ПІ - регулятора наведена на рис.1:

Рисунок 1. Крива розгону на виході об’єкта.
3. Обчислення і побудова комплексно-частотної характеристики (КЧХ) об’єкта
Перевід задачі в частотну область здійснюється шляхом формальної заміни повною комплексною незалежною змінною s її чисто комплексною частиною ωj:
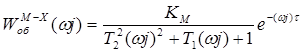
Дійсну і уявну частини КЧХ об’єкта по каналу регулювання можна визначити формулами:
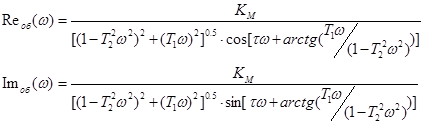
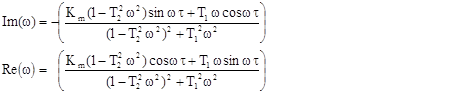
Для побудови КЧХ об’єкта без запізнення використовувались формули

На рис.2. наведені КЧХ об’єкту без запізнення та з запізненням.
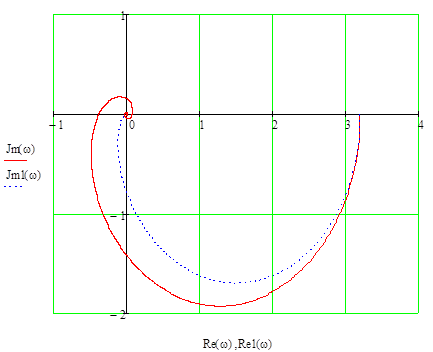
Рисунок 2. - КЧХ об’єкту:
a) з запізненням (суцільний); б) без запізнення (пунктирний).
4. Побудова межі cтiйкостi АСР
Вирази для визначення настройок, відповідних межі сталості АСР:

Кожному значенню колової частоти відповідає пара значень параметрів настройок Кр і Кр/ Тu . Для даної АСР межа області сталості повинна розташовуватися у верхній площині параметрів.